Énigmes
Miscellanées d'énigmes mathématiques.
Énigme 1
En marchant le long d'une rue, Pauline passe devant quatre maisons, toutes de couleurs différentes. Elle passe devant la maison orange avant la rouge et devant la bleue avant la jaune. La maison bleue n’est pas voisine de la jaune. De combien de manières différentes les maisons peuvent-elles être disposées ?
Solution
Notons O, R, B, J les quatre maisons.
- Contrainte 1 : on doit avoir O avant R
- Contrainte 2 : on doit avoir B avant J
- Contrainte 3 : de plus B n'est pas voisine de J donc O ou R est entre B et J
On en déduit les configurations possibles dans le sens de la marche de Pauline :
- si O et R entre B et J, une seule configuration compatible avec les trois contraintes :
- B O R J
- si O entre B et J :
- B O J R
- si R entre B et J :
- O B R J
Au total, les maisons peuvent être disposées de trois façons différentes.
Énigme 2
Quelle est la quantité maximale de carrés unitaires que l'on peut choisir de sorte que deux quelconques d'entre eux n'aient ni sommet ni côté en commun ?
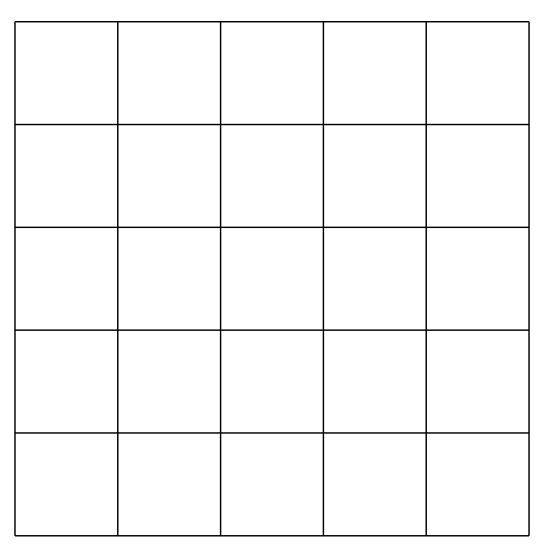
Solution
On a \(6 \times 6\) sommets donc au plus \(\frac{36}{4}=9\) carrés dont tous les sommets sont distincts. Ceci nous donne un majorant. Si on choisit les carrés des colonnes impaires sur les lignes impaires, on a exactement 9 carrés dont les sommets et les arêtes sont tous distincts donc le maximum est atteint.
Énigme 3
On lance trois dés. Quelle est la probabilité que la somme soit strictement supérieure à 15 ?
Solution
La somme de trois dés est strictement supérieure à 15 si et seulement si elle est égale à 16, 17 ou 18 :
- \(18=6+6+6\) une décomposition
- \(17 = 6+6+5 = 6+5+6 = 5+6 + 6\) trois décompositions
- \(16 = 6+ 5 + 5 = 5 + 6 + 5 = 5 + 5 + 6 = 6 + 6 + 4 = 6 + 4 + 6 = 4 + 6 + 6\) six décompositions
On a \(6 \times 6 \times 6 = 216\) issues équiprobables, les triplets de résultats des trois lancers ce qui nous donne une probabilité de \(\frac{10}{216}=\frac{5}{108}\).
Énigme 4
Il existe un pays dans lequel il n'existe que des pièces de 5 et des pièces de 7. Quelle est la quantité maximale que l'on ne peut pas obtenir avec ces deux types de pièces ?
Solution
On commence par une exploration algorithmique :
#!/usr/bin/python3
def est_decomposable(n, a, b):
"""Renvoie un booléen indiquant si n décomposable
comme n = a * x + b * y
"""
while n >= 0 and n % 7 != 0:
n = n - 5
return n >= 0
def liste_decomposable(a, b, bsup):
"""Renvoie la liste des entiers <= bsup non décomposables
sous la forme a*x + b * y"""
return [n for n in range(bsup) if not est_decomposable(n,a,b) ]
print(liste_decomposable(5, 7, 100))
renvoie :
[1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18, 23]
La série 24, 25, 26, 27, 28 est la première série de cinq entiers tous décomposables sous la forme \(7x+5y\). Tous les entiers suivants peuvent s'écrire sous la forme \(24+5a\), \(25+5b\), \(26+5c\), \(27+5d\) ou \(28+5e\) donc sont décomposables sous la forme \(7x+5y\).
C'est un cas particulier du problème de Frobenius dont un autre cas particulier célèbre est constitué par les Nombres Mc Nuggets.
Video
Énigme 5
Quatre couples ont réservé pour dîner dans un restaurant. Toutes les personnes arrivent au restaurant séparément. Combien d'entre elles doivent arriver afin d'être sûr que, au minimum, un couple soit présent ?
Solution
On applique le principe des tiroirs :
- On a 4 couples soit 4 tiroirs.
- Chaque personne arrivant séparément au hasard appartient à un couple donc à un tiroir.
À partir de 5 personnes, on a au moins deux personnes dans le même tiroir et donc au moins un couple.