Rentrée
Séance du 02/09/2016
Chapitre 1 : Second degré
- Présentation du programme, des objectifs, consignes de matériel (1 cahier grand format pour le cours et un cahier d'exercices, calculatrice)
- Cours :
- Formes d'une fonction polynome du second degré
- Position relative de 2 courbes : exemple 1
- DM1 pour mardi 06/09/2016
Séance du 05/09/2016
Chapitre 1 : Second degré
- Récolte du DM1 .
- Cours :
- Formes d'une fonction polynome du second degré
- Position relative de 2 courbes : fin de l'exemple 1
- Définition d'une fonction polynome du second degré.
- Applications : exemple 2 identification des coefficients
- Algorithmique et forme canonique exemple 3
- Différentes formes d'une fonction polynome du second degré :
- Propriété de mise sous forme canonique avec preuve ROC
- Applications de la mise sous forme canonique exemple 4 pas terminé
- Mettre sous forme canonique sur les exemples suivants (voir aussi
le Savoir Faire 1 page 13 du manuel) :
- \(x^2-6x + 5 \)
- \(2x^2-12x + 5 \)
- \(-2x^2+12x + 5 \)
Séance du 06/09/2016
Chapitre 1 : Second degré
- Récolte du DM1 .
- Cours :
- Forme canonique : fin de l'exemple 4
- Faire l'exemple 5 du cours.
- Ds sur le Second Degré le vendredi 23/05
Séance du 08/09/2016
Chapitre 1 : Second degré
- Cours :
- Propriétés de symétrie et des variations : application avec l'exemple 5 1., 2. et 3. seulement.
- Rappels sur la résolution d'équations par factorisation puis règle du produit nul exemple 7
- Théorème fondamental de résolution d'une équation du second degré sans preuve pour l'instant
- NOUVEAU : correction de quelques exercices du manuel ou de la fiche d'exercices
- Lire le Savoir Faire 2 page 13 et résoudre les exercices 46,47, 50 pages 20 et 21.
- Saisir dans sa calculatrice le programme
TRINOMEde résolution d'une équation du second degré donné ci-dessous pour une calculatrice TI - DS sur le Second Degré le vendredi 23/09
| Debut | Fin |
|---|---|
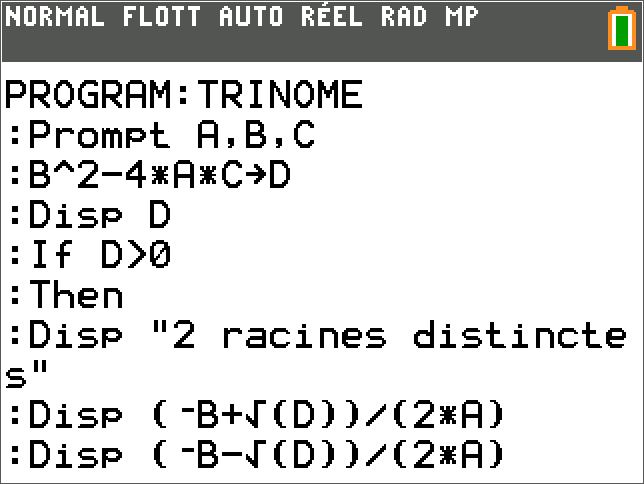 |
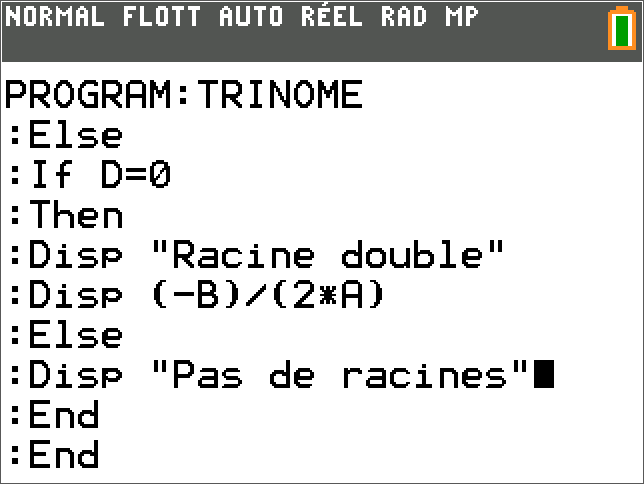 |
Séance du 12/09/2016
Chapitre 1 : Second degré
Cours en classe entière
- Correction des exercices46,47, 50 pages 20 et 21 : application du théorème fondamental sur la résolution d'équation du second degré.
- Cours :
- Théorème fondamental de résolution d'une équation du second degré sans preuve pour l'instant
- Application des formules de résolution : exemple 8.
- Preuve ROC du théorème fondamental.
- NOUVEAU : correction de quelques exercices du manuel ou de la fiche d'exercices
AP
- Faire l'exo 8 de la fiche 1, questions 1 à 10.
- DS sur le Second Degré le vendredi 23/09
Séance du 13/09/2016
Chapitre 1 : Second degré
- Correction de l'exo 8 de la fiche 1, questions 1 à 10.
- Cours :
- Exemple 9 : équations avec changement d'inconnue.
- Une figure Geogebra pour visualiser l'effet des coefficients \(a\), \(\alpha\) et \(\Delta\) sur la convexité et le nombre de points d'intersection avec l'axe des abscisses d'une parabole d'équation \(y=a\left((x-\alpha)^2-\frac{\Delta}{4a^2}\right)\).
- NOUVEAU : correction de quelques exercices du manuel ou de la fiche 1
- Faire les exos 4 et 6 de la fiche 1.
- DS sur le Second Degré le vendredi 23/09
Séance du 15/09/2016
Chapitre 1 : Second degré
- Cours : exemple 9 : équations avec changement d'inconnue, fin.
- Correction de l'exo 6 (intersection parabole/droite, paramètre) de la fiche 1.
- Cours :
- Inéquations du second degré : théorème 2 .
- Une figure Geogebra pour visualiser l'effet des coefficients \(a\), \(\alpha\) et \(\Delta\) sur la convexité et le nombre de points d'intersection avec l'axe des abscisses d'une parabole d'équation \(y=a\left((x-\alpha)^2-\frac{\Delta}{4a^2}\right)\).
- Exercices sur le signe d'un trinome : exos 22 à 29 p.19
- correction de quelques exercices du manuel ou de la fiche 1
- Finir les exos 22 à 29 p.19
- Lire les Savoir Faire 5 et 6 p. 15
- DS sur le Second Degré le vendredi 23/09
Séance du 16/09/2016
Chapitre 1 : Second degré
- Correction les exos 22 à 29 p.19 sur le signe d'un trinome.
- Correction de l'exo 4 (modélisation/variation).
- Exercice de logique : soit le trinome \(T: x \mapsto -x^{2}+bx-3\)
- L'implication (I)est-elle vraie : (I) Si \( -2\sqrt{3} < b < 2\sqrt{3} \) alors le trinome T n'a pas de racines.
- Que peut-on dire de \(b\) si le trinome a des racines ?
- La réciproque de l'implication (I) est-elle vraie ?
- correction de quelques exercices du manuel ou de la fiche 1
- Faire l'exemple 10 du cours.
- DS sur le Second Degré le vendredi 23/09
Séance du 19/09/2016
Chapitre 1 : Second degré
- Cours : correction de l'exemple 10 (signe d'un trinome, inéquations, positions relatives de courbes, étude d'une fonction bénéfice).
- correction de quelques exercices du manuel ou de la fiche 1
Chapitre 2 : Fonctions
- Cours :
- 1 Rappels :
- 1.1 Sens de variation : rappels des définitions formelles et applications dans l'exemple 1 (Vrai/Faux)
- 1 Rappels :
- Faire les exos 10 et 8 question 15) de la fiche 1.
- DS sur le Second Degré le vendredi 23/09
Séance du 20/09/2016
Chapitre 1 : Second degré
- Correction des exos 10 et 8 question 15) de la fiche 1.
- correction de quelques exercices du manuel ou de la fiche 1
Chapitre 2 : Fonctions
- Cours :
- 1 Rappels :
- 1.2 Fonctions usuelles de seconde (exemple 2) : tableaux de variations
- Exemple 3 : sens de variation et inégalités
- 1 Rappels :
- DS sur le Second Degré le vendredi 23/09
- Pour lundi 26/09 : DM n°2 à rendre sur feuille.
Séance du 23/09/2016
DS n°1 sur le chapitre Second degré.
- Pour lundi 26/09 : DM n°2 à rendre sur feuille.
Séance du 26/09/2016
Chapitre 2 : Fonctions
- Récolte du DM n°2.
- Cours :
- 1 Rappels :
- Exemple 3 : sens de variation et inégalités, étude du sens de variation de la fonction \(f: x \mapsto x^3\).
- 2 Fonction valeur absolue :
- 2.1 Définition comme distance à 0 et exemple 4 (enlever les barres de valeur absolue)
- Propriétés et définition comme fonction affine par morceaux \(| x | =\begin{cases} x\text{ si } x \geqslant 0 \\ -x \text{ si } x<0\end{cases}\), puis exemple 5 (algorithmique) et exemple 6 (résolution d'équations et d'inéquations).
- 1 Rappels :
AP : Logique, égalités, équations
- Faire les exos 10,11,12,15,16 p. 44.
Séance du 27/09/2016
Chapitre 2 : Fonctions
- Retour du DS n°1.
- Correction des exos 10,11,12,15,16 p. 44.
- Cours :
- 2 Fonction valeur absolue :
- Exemple 6 (résolution d'équations et d'inéquations).
- 2.2 Propriétés algébriques de la valeur absolue : propriété 2 et exemple 7.
- 2.3 Valeur absolue et intervalles : propriété 3 et exemple 8 (dont algorithmique)
- 2 Fonction valeur absolue :
- Faire l'exo 1 de la fiche d'exercices 2 sur la position relative de courbes.
Séance du 29/09/2016
Chapitre 2 : Fonctions
- Correction des exos 10,11,12,15,16 p. 44.
- Cours :
- 2 Fonction valeur absolue :
- Exemple 6 (résolution d'équations et d'inéquations), fin (4)).
- 2 Fonction valeur absolue :
- Faire l'exo 3 de la fiche d'exercices 2 sur les valeurs absolues.
Séance du 30/09/2016
Chapitre 2 : Fonctions
- Retour du DM n°2.
- Correction des exos 1 et 3 de la fiche d'exercices 2 .
- Cours :
- 2 Fonction valeur absolue :
- 2.2 Propriétés algébriques de la valeur absolue : propriété 2 et exemple 7 2).
- 2 Fonction valeur absolue :
- Faire l'exo 6 de la fiche d'exercices 2 .
Séance du 03/10/2016
Chapitre 2 : Fonctions
- Cours :
- 2 Fonction valeur absolue :
- 2.3 Valeur absolue et intervalles : propriété 3 et exemple 8 (dont algorithmique)
- 2 Fonction valeur absolue :
- Correction de l'exo 6 de la fiche d'exercices 2 : encadrement par balayage de la solution d'une équation \(f(x)=0\).
- Faire l'exemple 9 du cours sur les calculs avec la fonction racine carrée.
- DS d'1 h 30 le lundi 10/10/2016 portant sur les deux premiers chapitres.
Séance du 04/10/2016
Chapitre 2 : Fonctions
- Cours : 3 Fonction racine carrée 3.1 Définition et propriétés algébriques
- Théorème et propriétés 4 et 5, exemples 9 et 10 (transformations d'expressions, expressions conjuguées).
- Faire l'exo 4 de la fiche d'exercices 2 .
- Exercices d'application directe sur la fonction racine carrée : exos 20,21,22,25 p. 45 du manuel.
- DS d'1 h 30 le lundi 10/10/2016 portant sur les deux premiers chapitres.
Séance du 07/10/2016
Chapitre 2 : Fonctions
- Cours : 3 Fonction racine carrée 3.1 Définition et propriétés algébriques
- Expressions conjuguées : Exemple 1) c)
- Courbe et sens de variation de la fonction carré avec preuve ROC.
- Application des variations de la fonction racine carrée : exemple 11.
- DS d'1 h 30 le lundi 10/10/2016 portant sur les deux premiers chapitres, la fonction racine carrée n'est pas au programme
- Pour mardi : faire l'exo 5 de la fiche d'exercices 2 .
Séance du 10/10/2016
Matin : DS n°2 sur les chapitres Second degré et Compléments sur les Fonctions.
Après-midi : Chapitre 2 : Fonctions
- Correction de l'exo 4 de la fiche d'exercices 2 .
- Cours : 3 Fonction racine carrée 3.1 Définition et propriétés algébriques
- Application des variations de la fonction racine carrée : fin de l'exemple 11.
- Comparaisons des fonctions \(x \mapsto x\), \(x \mapsto x^2\) et \(x \mapsto \sqrt{x}\) : propiété avec preuve ROC et exemple 12.
- Pour mardi : faire l'exo 5 de la fiche d'exercices 2 .
- Vendredi : AP en salles informatiques 716 et 717.
Séance du 11/10/2016
Après-midi : Chapitre 2 : Fonctions
- 4 Opérations sur les fonctions
- Fonctions \(u+\lambda\) et \(\lambda u\) et sens de variation : définition, propriétés avec preuve, exemple 13.
- Fonctions \(\frac{1}{u}\) et \(\sqrt{u}\) et sens de variation : propriété et exemple 14.
- Pour jeudi : faire les exos 73 à 75 page 49 puis l'exo 84 page 49.
- Vendredi : AP en salles informatiques 716 et 717.
Séance du 13/10/2016
Après-midi : Chapitre 2 : Fonctions
- Correction des exercices 73 à 75 page 49 puis du 84 page 49.
- Cours : Fonctions \(u+v\) et \(uv\) et sens de variation : propriétés 12 et 13 + exemple 15.
- Pour le jeudi de la rentrée DM N°3
- Vendredi : AP en salles informatiques 716 et 717.
Séance du 14/10/2016
Séance du 17/10/2016
Chapitre 3 : Suites Partie 1
- Cours :
- 1. Notion de suite 1.1 Activité d'introduction (commencée en TP vendredi dernier) : correction (calculs de termes à la main + algorithme de calcul du terme de rang \(n\) d'une suite récurrente + algorithme de seuil + programmation de la calculatrice).
- Calcul des termes d'une suite avec la calculatrice : fiche TICE p. 122 du manuel.
- Définition d'une suite numérique + exemple 2 : quelques exemples élémentaires de suites définies par extension, récurrence ou par uune formule explicite.
- Programmer sur sa calculatrice les deux algorithmes de l'exemple 1 (Activité d'introduction).
- Faire les exercices de base : exos 4,7,10, 11 p. 124.
- Pour le jeudi de la rentrée DM N°3
- Lundi 7/11 : DS de 2 heures sur tous les Chapitres vus depuis la rentrée, pour le chapitre Suites, les révisions s'arretent à la manipulation des différentes définitions d'une suite (paex récurrence, par formule explicite) et au calcul de termes à la main, avec le tableur, avec le mode suite de la récurrence ...
Séance du 18/10/2016
Chapitre 3 : Suites Partie 1
- Correction des exercices de base : exos 4,7,10, 11 p. 124.
- Cours :
- Vérification des programmes de l'exemple 1.
- Exemple 3 : définition de la suite des entiers impairs de plusieurs façons : par extension 1, 3, 5, 7 ou par récurrence \(u(n+1)=u(n)+2\) ou par une formule explicite \(u(n)=2n+1\).
- Calculs de termes d'une suite récurrente : exercice 1 de la Fiche 3 ..
- Pour le jeudi de la rentrée DM N°3
- Lundi 7/11 : DS de 2 heures sur tous les Chapitres vus depuis la rentrée, pour le chapitre Suites, les révisions s'arretent à la manipulation des différentes définitions d'une suite (par récurrence, par formule explicite) et au calcul de termes à la main, avec le tableur, avec le mode suite de la récurrence ...
Toussaint
Séance du 04/11/2016
Chapitre 3 : Suites Partie 1
- Récolte du DM n°3. A propos du nombre d'Or, voir cette animation que j'ai écrite en Snap sur les Rectangles et la spirale d'Or .
- Cours :
- Vérification des programmes de l'exemple 1.
- Exemple 4 : calculs de termes successifs de la suite récurrente \(\begin{cases} u_{0} = 600 \\ u_{n+1} = 0,7u_{n}+210 \end{cases} \)
- Calculs de termes d'une suite récurrente avec le mode suite de la calculatrice : exercice 2 de la Fiche 3 et exercice ci-dessous :
Soit la suite \((u_{n})\) définie par : \(u_0 = 16\) et, pour tout entier \(n \geqslant 0\), \(u_{n+1} = \sqrt{u_n} + n\).
- Détailler le calcul des valeurs exactes des termes \(u_{1}\) et \(u_{2}\).
- Déterminer avec le mode
Suitede la calculatrice une valeur décimale approchée à \(10^{-3}\) près de \(u_{20}\). - Déterminer le plus petit entier \(n\) tel que \(u_{n}>30\). Expliquer la démarche employée.
- Lundi 7/11 : DS de 2 heures sur tous les Chapitres vus depuis la rentrée, pour le chapitre Suites, les révisions s'arretent à la manipulation des différentes définitions d'une suite (paex récurrence, par formule explicite) et au calcul de termes à la main, avec le tableur, avec le mode suite de la récurrence ...
Séance du 07/11/2016
Matin DS n°3 (2 h) sur Second Degré, Fonctions, Suites
Chapitre 3 : Suites Partie 1
- A propos du nombre d'Or, voir cette animation que j'ai écrite en Snap sur les Rectangles et la spirale d'Or .
- Cours : 2 Suites arithmétiques.
- Définition et exemple 5.
- Calculs de termes, représentation graphique et exemple 6.
- Exercices d'application directe sur les suites arithmétiques : exercices 27, 28, 30, 31 p. 125.
- Faire les exercices 27, 28, 30, 31 p. 125 et 5 de la Fiche 3 ..
Séance du 08/11/2016
Chapitre 3 : Suites Partie 1
- A propos du nombre d'Or, voir cette animation que j'ai écrite en Snap sur les Rectangles et la spirale d'Or .
- Cours : 2 Suites arithmétiques.
- Calculs de termes, représentation graphique et exemple 6 (fin).
- Correction des exercices d'application directe sur les suites arithmétiques : exercices 27, 28, 30 p. 125 et de l'exercice 5 de la Fiche 3 .. puis .
- Cours : somme des termes consécutifs d'une suite arithmétique, propriété avec preuve ROC puis exemple 7.
- Faire les exercices 32 p. 125, 71, 75 p. 128 Répondre au problème du décompte des allumettes dans une pyramide.
- Mardi 08/11 de 13h à 14 h en salles 715 et 716 : Concours Castor Informatique .
Séance du 10/11/2016
Chapitre 3 : Suites Partie 1
- Retour du DM n°3.
- A propos du nombre d'Or, voir cette animation que j'ai écrite en Snap sur les Rectangles et la spirale d'Or .
- Cours : somme des termes consécutifs d'une suite arithmétique, retour sur la fin de la preuve ROC puis exemple 7.
- Correction des exercices 32 p. 125, 71, et du problème du décompte des allumettes dans une pyramide.
- Mardi 15/11 de 12h à 13 h en salle 715 : Concours Castor Informatique .
- Pour lundi 13/11 : faire les exos 78 et 85 p. 129, 113 p. 131 et l'exo 3 de la Fiche 3 .
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 14/11/2016
Chapitre 3 : Suites Partie 1
- Retour du DS n°3.
- Suites arithmétiques : correction des exos 78, 85 .p 129 et 113 p. 131 .
- Cours : Suites géométriques : définition d'une suite géométrique, propriétés de calculs de termes, exemple 8
- Mardi 15/11 de 12h à 13 h en salle 715 : Concours Castor Informatique .
- Pour mardi 15/11 : faire les exos 92, 93 et 97 p. 130. .
- Pour lundi 21/11 : DM n°4.
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 15/11/2016
Chapitre 3 : Suites Partie 1
- Distribution du corrigé du DS n°3.
- Suites arithmétiques : correction de l'exo 3 de la Fiche 3 .
- Suites géométriques : correction des exos d'application 92,93,97 p. 130.
- Cours : somme des termes consécutifs d'une suite géométrique : propriété 8 avec preuve ROC.
- Mardi 15/11 de 12h à 13 h en salle 715 : Concours Castor Informatique .
- Pour lundi 21/11 : DM n°4.
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 18/11/2016
Chapitre 3 : Suites Partie 1
- Cours : somme des termes consécutifs d'une suite géométrique : propriété 8 avec preuve ROC (fin).
- Somme des termes consécutifs d'une suite géométrique, application directe, exercice 38 p. 125.
- Cours : somme des termes consécutifs d'une suite géométrique, exemple 10 et début de l'exemple 11.
- Pour lundi 21/11 : DM n°4.
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 19/11/2016
Chapitre 3 : Suites Partie 1
- Cours : somme des termes consécutifs d'une suite géométrique : propriété 8 avec preuve ROC (fin).
- Somme des termes consécutifs d'une suite géométrique, application directe, exercice 38 p. 125.
- Cours : somme des termes consécutifs d'une suite géométrique, exemple 10 et début de l'exemple 11.
- Pour lundi 21/11 : DM n°4.
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 21/11/2016
Rencontre avec des chercheurs dans le cadre du protocole Déclics .
Chapitre 3 : Suites Partie 1
- Récupération du DM n°4.
- Cours : somme des termes consécutifs d'une suite géométrique, exemple 11 (tapis de Sierpinski).
- Pour mardi 22/11 : faire l'exo 3 de la fiche 4 .
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 22/11/2016
Chapitre 3 : Suites Partie 1
- Exercice 3 (suite géométrique et algorithme de seuil) puis exercice 4 (suite arithmético-géométrique et algorithme de seuil) de la fiche 4 .
- Pour jeudi 24/11 : faire l'exo 5 de la fiche 4 et les exos 104 et 105 p. 130 .
- Lundi 28/11 ou Mardi 29/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 24/11/2016
Chapitre 3 : Suites Partie 1
- Suites géométriques : correction des exercices du manuel 104 et 105 p. 130.
- Suites arithmético-géométriques (représentation graphique, algorithmique, conjectures sur le comportement asymptotique) : correction de l'exo 5 de la fiche 4
- Pour vendredi 25/11 : faire les exos 114 p.131 et l'exo 6 de la fiche 4 .
- Lundi 28/11 : DS d'une heure sur le chapitre Suites.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 25/11/2016
Chapitre 3 : Suites Partie 1
- Correction de l'exo 114 p. 131.
- Suites arithmético-géométriques (représentation graphique, algorithmique, conjectures sur le comportement asymptotique) : fin de la correction de l'exo 5 de la fiche 4
- Un exercice similaire à l'exemple 11 du cours : l'exercice 6 de la de la fiche 4 , avec l'étude du triangle de Sierpinski. Voir aussi mon animation Snap autour de la courbe de Sierpinski .
- Lundi 28/11 : DS d'une heure sur le chapitre Suites en salle 432.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 28/11/2016
DS d'une heure sur les suites.
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Cours 1 Bases et repères du plan :
- 1.1 Rappels sur les vecteurs puis exemples 1 (démontrer un alignement par calcul vectoriel) et 2 (caractérisation du centre de gravité).
- Pour mardi : finir les exemples 1 et 2.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 29/11/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Cours : 1 Bases et repères du plan :
- 1.1 Rappels sur les vecteurs puis exemples 1 (démontrer un alignement par calcul vectoriel) et 2 (caractérisation du centre de gravité).
- 1.2 Bases et repères du plan : rappels puis exemple 3 qui reprend l'exemple 1 avec une méthode analytique.
- Pour vendredi : finir l'exemple 3 de la fiche de cours et faire l'exo 1 de la fiche d'exos
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 02/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Cours : 1 Bases et repères du plan :
- 1.2 Bases et repères du plan : fin de la correction de l'exemple 3 qui reprend l'exemple 1 avec une méthode analytique.
- Cours : 1.3 Critère analytique de colinéarité : Propriété, exemple 5.
- Pour lundi : faire les exos 103 p. 130, 134 p. 139 et 85 p. 49 (exercice corrigé).
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année.
Séance du 05/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Révisions pour le devoir commun : correction des exos 103 p. 130, 134 p. 139.
- Exercices : correction de l'exo 1 de la fiche d'exos .
- Cours : 1.3 Critère analytique de colinéarité : Propriété, fin de l'exemple 5, puis algorithme pour déterminer si trois points sont alignés.
- Un exercice sur les équations réduites de droites :
Dans un repère du plan on considère les points A(-5,5) B(-3,-3) et C(5,7) Démontrer qu'une équation de la médiane issue de A est y=5/2-x/2 Déterminer une équation de la médiane issue de B En déduire les coordonnées du centre de gravité G du triangle ABC
AP : Révisions pour le Devoir Commun
- Pour mardi : finir l'exo rédigé au tableau, faire l'exo 101 p.156 et faire l'exo 3 de la la fiche AP : Révisions pour le Devoir Commun.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année (sauf les vecteurs).
Séance du 06/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Correction de l'exo 3 de la la fiche AP : Révisions pour le Devoir Commun (sur les suites arithmétiques).
- Correction de l'exercice suivant sur les équations réduites de droites :
Dans un repère du plan on considère les points A(-5,5) B(-3,-3) et C(5,7) Démontrer qu'une équation de la médiane issue de A est y=5/2-x/2 Déterminer une équation de la médiane issue de B En déduire les coordonnées du centre de gravité G du triangle ABC - Cours 2 Equations de droites :
- Vecteur directeur et équation cartésienne \(ax+by+c=0 \) : définitions, propriété de l'équation cartésienne d'une droite.
- Exercices d'applications directes sur les vecteurs directeurs et les équations cartésiennes de droites : exo 25 p. 151.
- Méthodes pour déterminer une équation de droites : Les trois façons de déterminer une équation de droite
- Pour jeudi : faire les exos 26,27,28 p.151 et les exos 94, 97 p. 156.
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10h, révisions portant sur tout ce qui a été vu depuis le début de l'année (sauf les vecteurs).
Séance du 08/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Vecteur directeur et équation cartésienne \(ax+by+c=0 \) : correction des exos 26,27,28 p.151 et des exos 94, 97 p. 156.
- Méthodes pour déterminer une équation de droites : Les trois façons de déterminer une équation de droite
- Pour vendredi : préparer l'exemple 6 de la fiche de cours .
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10 h en salle 433, révisions portant sur tout ce qui a été vu depuis le début de l'année (sauf les vecteurs).
Séance du 09/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Cours 2 Equations de droites :
- Vecteur directeur et équation cartésienne \(ax+by+c=0 \) : correction de l'exemple 6.
- Méthodes pour déterminer une équation de droites : Les trois façons de déterminer une équation de droite
- Lundi 12/12 : Devoir commun de deux heures de 8 h à 10 h en salle 433, révisions portant sur tout ce qui a été vu depuis le début de l'année (sauf les vecteurs).
Séance du 12/12/2016
Devoir Commun de 2 h.
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Applications directes, déterminer une équation de droite :
- A partir d'un point et d'un vecteur directeur :99 p. 156.
- A partir de deux points : 104 p. 156.
- Cours :
- Equation réduite d'une droite
- Caractérisation du parallélisme : Propriété 6 avec preuve ROC.
- Méthodes pour déterminer une équation de droites : Les trois façons de déterminer une équation de droite
- Pour mardi 13/12 : exos 3 et 6 de la fiche d'exos et l'exemple 7 du cours.
- Pour le mardi 03/01 : DM n° 5
Séance du 13/12/2016
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Cours :
- Equation réduite d'une droite
- Caractérisation du parallélisme : correction de l'exemple 7.
- Correction de l'exo 3 de la fiche d'exos .
- Un peu de géométrie dans l'espace : exo 12 de la fiche d'exos
- Méthodes pour déterminer une équation de droite : Les trois façons de déterminer une équation de droite
- Pour vendredi 13/12 : finir l'exo 12 de la fiche d'exos et faire les exercices de synthèse : 133 p. 15 ( équation d'une parallèle) et exo 132 p. 157. (équation d'une médiane) et l'exo 130 p. 157 (critère de colinéarité).
- Vendredi 13/12 : TP en salle informatique, amener le manuel.
- Pour le mardi 03/01 : DM n° 5
Séance du 16/12/2016
TP INFO n° 2
- Section d'un cube (fin de l'exo 12 de la fiche d'exos ).
- Correction des exos TOP CHRONO de la page 157.
- TP2 page 162 : enveloppes de droites. Cliquez sur ce lien pour accéder au corrigé.
- Méthodes pour déterminer une équation de droite : Les trois façons de déterminer une équation de droite
- Pour le mardi 03/01 : DM n° 5
Noel
Séance du 03/01/2017
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Retour du Devoir Commun du lundi 12/12.
- Bilan du chapitre, préparation du DS n°6 à travers une fiche d'exercices préparatoire du DS 6.
- Rappels, exercices corrigés sur le chapitre Colinéarité et équations de droites :
- Méthodes pour déterminer une équation de droite : Les trois façons de déterminer une équation de droite
- Correction des exos TOP CHRONO de la page 157.
- Pour le jeudi 05/01 : finir les exercices de la fiche d'exercices préparatoire du DS 6. et apporter le manuel. .
- Pour le vendredi 06/01 : DM n° 5
- Pour le lundi 16/01 : DS n°6 sur le chapitre Colinéarité et Equations de droites (avec un exercice sur les suites géométriques ou arithmétiques).
Séance du 05/01/2017
Chapitre 4 : Vecteurs et Colinéarité, Equations de droites
- Bilan du chapitre, fin de la correction de la fiche d'exercices préparatoire du DS 6.
- Rappels, exercices corrigés sur le chapitre Colinéarité et équations de droites :
- Méthodes pour déterminer une équation de droite : Les trois façons de déterminer une équation de droite
- Correction des exos TOP CHRONO de la page 157.
Chapitre 5 : Dérivation
- Notion de vitesse instantanée : Activité 1 page 62 du Chapitre 3 Dérivation du manuel.
- Corrigé de l'activité 1 page 62. .
Séance du 06/01/2017
Chapitre 5 : Dérivation
- Récolte du DM n° 5.
- Notion de vitesse instantanée : Activité 1 page 62 du Chapitre 3 Dérivation du manuel.
- Corrigé de l'activité 1 page 62. .
- Cours :
- 1 Nombre dérivé 1.1 Taux d'accroissement exemple 1, 1.2 Fonction dérivable Exemple 2 : cas de la fonction carré \(f: x \mapsto x^2 \) en 1
- Préparer l'exemple 2 du cours.
- Pour le vendredi 13/01 : DM n° 6
- Pour le lundi 16/01 : DS n°6 sur le chapitre Colinéarité et Equations de droites (avec un exercice sur les suites géométriques ou arithmétiques).
Séance du 09/01/2017
Chapitre 5 : Dérivation
- Présentation des Olympiades de Mathématiques et appel à candidature.
- Corrigé de l'activité 1 page 62. .
- Cours :
- 1 Nombre dérivé 1.1 Taux d'accroissement exemple 1, 1.2 Fonction dérivable Exemple 2 : cas de la fonction carré \(f: x \mapsto x^2 \) en 1
- Corrigé de l'exemple 2 .
- Exemple 3 : dérivée de \(f: x \mapsto x^2 \) en 3 et tangente à sa courbe au point \( (3, f(3)) \)
- Calculs de nombres dérivés et tangentes : exercices 1,2, 3, 4, 5 p. 70.
- Finir les exercices 1,2,3,4,5,7 p.70 .
- Pour le vendredi 13/01 : DM n° 6
- Pour le lundi 16/01 : DS n°6 sur le chapitre Colinéarité et Equations de droites (avec un exercice sur les suites géométriques ou arithmétiques).
Séance du 10/01/2017
Chapitre 5 : Dérivation
- Calculs de nombres dérivés : exercices 1,2, 3, 4, 5 p. 70.
- Cours :
- 1.3 Tangente à la courbe d’une fonction dérivable : Propriété puis exemple 4.
- Pour le vendredi 13/01 : DM n° 6
- Pour le lundi 16/01 : DS n°6 à 9h en salle 433 sur le chapitre Colinéarité et Equations de droites (avec un exercice sur les suites géométriques ou arithmétiques).
Séance du 13/01/2017
Chapitre 5 : Dérivation
- Récolte du DM n° 6
- Cours :
- 1.3 Tangente à la courbe d’une fonction dérivable : fin de l'exemple 4.
- 2 Fonction dérivée : Définition 3, Exemple 5 : nombre dérivé en \(a\) de \(f:x \mapsto x^3\).
- Pour le lundi 16/01 : DS n°6 à 9h en salle 433 sur le chapitre Colinéarité et Equations de droites (avec un exercice sur les suites géométriques ou arithmétiques).
Séance du 16/01/2017
DS n° 6 sur le calcul vectoriel, les équations de droites et les suites.
Chapitre 5 : Dérivation
- Cours :
- 2 Fonction dérivée : Définition 3, fin de l'exemple 5 : nombre dérivé en \(a\) de \(f:x \mapsto x^3\).
- 2.2 Dérivées des fonctions usuelles : tableau des dérivées des fonctions usuelles.
- Applications des formules de dérivation des fonctions usuelles : exos 8,9,11,12,13 pages 70 et 71.
- Nombre dérivé en 1 puis en \( a \neq 0 \) pour \( f : x \mapsto \frac{1}{x} \) : exercice 1 de la fiche 1 sur la dérivation. .
- Applications des formules de dérivation, exos 17,18,19,20,21,22,24,26 page 71.
- Pour le mardi 17/01 :
- Exercice 1 soit la fonction définie sur R par \(f: x \mapsto x^2\). Démontrer que pour tout réel a, f est dérivable en a et que \(f'(a) = 2 a\).
- Exercice 2 soit la fonction définie sur R par \(f: x \mapsto mx+p\) avec m et p des constantes. Démontrer que pour tout réel a, f est dérivable en a et que \(f'(a) = m\).
- Faire les exercices 35 p. 72 et 40 p. 73 (Nombre dérivé comme coefficient directeur de tangente)
Séance du 17/01/2017
Chapitre 5 : Dérivation
- Retour du DM n° 6 .
- Nombre dérivé comme coefficient directeur de tangente : correction des exos 35 p. 72 et 40 p. 73 .
- Cours :
- 2.2 Preuve de des nombres dérivés en \(a\) (si la fonction est dérivable en \(a\) ) des fonctions affines, carré, inverse et racine carré.
- 2.2 Dérivées des fonctions usuelles : exemple 6 (exemple de deux fonctions non dérivables en 0, \(f;x \mapsto \sqrt{x}\) et \(g:x \mapsto \vert \, x \, \vert\))
- Pour le jeudi 19/01 : finir les exemples 6 et 7 du cours.
Séance du 19/01/2017
Chapitre 5 : Dérivation
- Cours :
- 2.2 Dérivées des fonctions usuelles : exemple 6 (exemple de deux fonctions non dérivables en 0, \(f;x \mapsto \sqrt{x}\) et \(g:x \mapsto \vert \, x \, \vert\)) et exemple 7 (équations de tangentes pour des courbes de fonctions usuelles) 1) et 2)
- 2.3 Opérations sur les fonctions dérivables : Propriété 2 (tableau)
- Applications des formules de dérivation, exos 17,18, 19,20 page 71.
- Pour le vendredi 20/01 : lire les Savoir Faire 3 , 4 page 67 et le Savoir Faire 5 1) et finir les exos 17, 18, 19, 20 page 71
Séance du 20/01/2017
Chapitre 5 : Dérivation
- Opérations sur les fonctions dérivables, applications des formules de dérivation :
- \(u + v \) et \( \lambda u \) : exos 17,18, 19,20 page 71.
- \(u v \), \(\frac{1}{v} \) : 21,22,24 page 71.
- Pour le lundi 23/01 : lire les Savoir Faire 5 et 6 page 59, faire l'exo 2 de la fiche 1 sur la dérivation. et les questions 1) à 10) de l'exo 5 de la fiche 1 sur la dérivation. . Voir un corrigé de l'exo 5.
Séance du 23/01/2017
Chapitre 5 : Dérivation
- Calculs de dérivée, équations de tangentes :
- correction de l'exo 2 de la fiche 1 sur la dérivation.
- correction de quelques questions de l'exo 5 de la fiche 1 sur la dérivation. . Voir un corrigé de l'exo 5.
- Opérations sur les fonctions dérivables, applications des formules de dérivation :
- \( \frac{u}{v} \) : exo 26 page 71.
- Fiche de
- Synthèse du chapitre : Fiche de Synthèse
- Pour le mardi 24/01 : question 6) de l'exercice 2 de la fiche de
- Synthèse du chapitre : Fiche de Synthèse et faire l'exo 7 de la fiche 1 sur la dérivation. .
- Pour le lundi 30/01 : DM n° 7
Séance du 24/01/2017
Chapitre 5 : Dérivation
- Fin de la fiche de
- Synthèse du chapitre : Fiche de Synthèse
- Cours :
- 2.3 Opérations sur les dérivées : Propriété 2, preuves des formules de dérivation d'une somme et d'un produit.
- Voir le corrigé de l'exo 119 p. 185
- Pour le vendredi 27/01 : faire l'exo 6 de la fiche 1 sur la dérivation. et calculer les dérivées des questions 11) 12) 17) et 18) de l'exo 5 de la fiche 1 sur la dérivation. . Voir un corrigé de l'exo 5.
- Pour le lundi 30/01 : DM n° 7
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
Séance du 27/01/2017
Chapitre 5 : Dérivation
- Correction de l'exo 7 de la fiche 1 sur la dérivation. .
- Cours :
- 2.3 Opérations sur les dérivées : Exemple 8 dérivabilité sur l'intervalle \([0 ; + \infty [\) de \( f : x \mapsto 4 x \sqrt{x} \).
- Pour les dérivées des questions 11) 12) 17) et 18) de l'exo 5 de la fiche 1 sur la dérivation. voir un corrigé de l'exo 5.
- Voir le corrigé de l'exo 119 p. 185
- Pour le lundi 30/01 : DM n° 7
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
Séance du 30/01/2017
Chapitre 5 : Dérivation
- Récolte du DM n° 7
- Fiche de préparation du DS n°7
- Pour les dérivées des questions 11) 12) 17) et 18) de l'exo 5 de la fiche 1 sur la dérivation. voir un corrigé de l'exo 5.
- Voir le corrigé de l'exo 119 p. 185
Chapitre 6: Statistiques
- Corrigé des exemples du cours
- Cours :
- 1 Vocabulaire
- 2 Caractérisation par le couple Moyenne/Ecart-type : définitions, propriétés et exemples 1 et 2.
Pas d'AP : cours supprimé pour cause de conférence sur la non violence.
- Pour le mardi 31 /01 : finir l'exo 4 de la Fiche de préparation du DS n°7 .
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
Séance du 31/01/2017
Chapitre 6: Statistiques
- Petit retour sur la dérivation : correction de l'exo 4 de la Fiche de préparation du DS n°7
- Corrigé des exemples du cours
- Cours :
- 2 Caractérisation par le couple Moyenne/Ecart-type : exemples 3 et 4 (utilisation des listes de la calculatrice).
- Pour le jeudi 02/02 : préparer les exemples 5 et 6 du Chapitre 6: Statistiques .
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
Séance du 02/02/2017
Chapitre 6: Statistiques
- Petit retour sur la dérivation : correction de l'exo 6 de la fiche 1 sur la dérivation.
- Retour du DM n° 7 .
- Corrigé des exemples du cours
- Cours :
- 3 Caractérisation par le couple Médiane/Ecart-interquartile : définition, propriétés et correction des exemples 5 et 6.
- Pour le vendredi 03/ 02 : préparer les exemples 7 et 8 du Chapitre 6: Statistiques .
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
Séance du 03/02/2017
Chapitre 6: Statistiques
- Corrigé des exemples du cours
- Cours :
- 3 Diagrammes en boites : définition, exemples 7, 8.
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Cours :
- 1. Rappels sur les lois de probabilité : définitions et propriétés.
- Lundi 6/02 : DS de 2 heures sur le Chapitre 5 : Dérivation
- Pour mardi 7/02 : préparer l'exemple 1 du Chapitre 7 : Variables aléatoires .
Séance du 06/02/2017
DS n° 7 sur la Dérivation (2 heures).
- Pour mardi 7/02 : préparer l'exemple 1 du Chapitre 7 : Variables aléatoires .
Séance du 07/02/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Cours :
- 1. Rappels sur les lois de probabilité : définitions et propriétés, correction de l'exemple 1.
- 2 Loi d'une variable aléatoire : exemple 2, définition.
- Pour vendredi 10/02 : faire les exercices 5,9, 11 et 12 page 278 du manuel
- Pour la semaine prochaine : DM facultatif Olympiades
- Pour le lundi 6/03 : DM n°8
Séance du 10/02/2017
Chapitre 7 : Variables aléatoires
- Retour du DS n°8.
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Cours :
- 2 Loi d'une variable aléatoire :exemple 3.
- Exercices sur la loi de probabilité d'une variable aléatoire : correction des exercices 5,9, 11 et 12 page 278 du manuel puis exercice 2 de la fiche d'exercices 1
- Cours :
- 3 Espérance d'une variable aléatoire : définition.
- Pour lundi 13/02 : faire les exercices 1, 2 et 3 de la fiche d'exercices 1 .
- Pour la semaine prochaine : DM facultatif Olympiades
- Pour le lundi 6/03 : DM n°8
Séance du 13/02/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Correction des exercices 1, 2 et 3 de la fiche d'exercices 1 .
- Cours :
- 3 Espérance d'une variable aléatoire : exemples 4 et 5.
- 3.2 Espérance comme valeur : exemple 6 puis loi faible des grands nombreS.
- 3.3 Variance et écart-type : définition 5 et propriété 3 (formule de Konig) et exemple 7.
AP
- Calcul de dérivée : exo 78 p. 76.
- Exercices sur espérance et écart-type : exercices 17,18 page 279 et exercices 46 et 50 p. 283.
- Pour mardi 13/02 : finir les exercices 17,18 page 279 et 46 et 50 p. 283.
- A rendre dans la semaine : DM facultatif Olympiades
- Pour le lundi 6/03 : DM n°8
Séance du 14/02/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Correction des exercices sur loi de probabilité, espérance et variance : 17,18 page 279 et 46 et 50 p. 283.
- Cours :
- 3.4 Espérance et variance de la variable aléatoire \(aX+b\) : propriété 4 et exemple 8 (écrit au tableau mais pas corrigé)
- Pour jeudi 16/02 : TP INFO en salles 715 et 716.
- Pour vendredi 17/02 : exemple 8 du cours.
- A rendre dans la semaine : DM facultatif Olympiades
- Pour le lundi 6/03 : DM n°8
Séance du 16/02/2017
- Pour vendredi 17/02 : exemple 8 du cours.
- A rendre dans la semaine : DM facultatif Olympiades
- Pour le lundi 6/03 : DM n°8
Séance du 17/02/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Récolte du DM facultatif Olympiades .
- Cours :
- 3.4 Espérance et variance de la variable aléatoire \(aX+b\) : propriété 4 et exemple 8 (correction)
- Exercices sur la linéarité de l'espérance : exos 52 et 53 p. 284.
- Cours :
- 4 Répétition d’expériences identiques et indépendantes, arbres pondé-
rés:
- Définition et exemple.
- Représentation par un arbre pondéré : exemple 10 (inachevé).
- 4 Répétition d’expériences identiques et indépendantes, arbres pondé-
rés:
- Pour le lundi 6/03 : DM n°8
- Lundi 13/03 : DS n° 8 de 2 h sur les chapitres Chapitre 6: Statistiques et Chapitre 7 : Variables aléatoires . Revoir aussi les formules de dérivation et l'équation d'une tangente.
Février
Séance du 06/03/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Récolte du DM n°8 .
- Cours :
- 4 Répétition d’expériences identiques et indépendantes, arbres pondé-
rés:
- Représentation par un arbre pondéré : exemple 10 (fin).
- Calcul de probabilité avec un arbre pondéré : probabilité d'une liste, lois des noeuds et des chemins.
- 4 Répétition d’expériences identiques et indépendantes, arbres pondé-
rés:
- Exercices sur la répétition d'expériences identiques et indépendantes :
- Exercices 21 et 23 p. 278.
- Exercices 57 p. 284 et 60 p.285.
- Exercice 6 de la fiche d'exercices 1
- Pour le mardi 7/03 : faire les exercices 70 et 64 page 285.
- Lundi 13/03 : DS n° 8 de 2 h sur les chapitres Chapitre 6: Statistiques et Chapitre 7 : Variables aléatoires . Revoir aussi le DM n°8 , l'exercice 78 page 76 (formule de dérivation de l'inverse) et l'équation d'une tangente.
Séance du 07/03/2017
Chapitre 7 : Variables aléatoires
- Corrigé des exemples du cours en HTML et Corrigé des exemples du cours en PDF
- Cours :
- 4 Répétition d’expériences identiques et indépendantes, arbres pondérés:
- Calcul de probabilité avec un arbre pondéré : exemple 12 (algorithmique).
- 4 Répétition d’expériences identiques et indépendantes, arbres pondérés:
- Corrigé des exos 61,62,64,70 p. 285 et 89 p. 293. .
- Lundi 13/03 : DS n° 8 de 2 h sur les chapitres Chapitre 6: Statistiques et Chapitre 7 : Variables aléatoires . Revoir aussi le DM n°8 , l'exercice 78 page 76 (formule de dérivation de l'inverse) et l'équation d'une tangente.
Séance du 13/03/2017
Séance du 14/03/2017
Chapitre 8 : Applications de la dérivation.
- Cours :
- Exemple 1 et théorème 1 : du sens de variation au signe de la dérivée.
- Exemples 2 et 3 et théorème 2 : du signe de la dérivée au sens de variation.
- Exercices du manuel :
- Du sens de variation au signe de la dérivée : exos 5,7 page 94.
- Du signe de la dérivée au sens de variation : exos 11 et 12 p. 94 et 18 p. 95 (étude des variations d'une fonction polynome du second degré).
- Finir les exos 28 page 96, 33 et 38 page 97 et l'exemple 2 du cours.
Séance du 16/03/2017
Chapitre 8 : Applications de la dérivation.
- Correction des exos 28 page 96, 33 et 38 page 97.
- Cours :
- Exemples 2 et 3 du cours (pas terminé)
- Méthode pour étudier les variations d'une fonction dérivable, définitions des extrema locaux ou globaux et exemple 4.
- Condition nécessaire mais pas suffisante d'extremum local : propriété et exemples 5 et 6 (variations d'une fonction rationnelle).
- Finir l'exemple 3 et faire l'exo 40 page 97.
Séance du 17/03/2017
Chapitre 8 : Applications de la dérivation.
- Correction de l'exo 40 page 97.
- Cours :
- Exemples 3 du cours (fin)
- Méthode pour étudier les variations d'une fonction dérivable, définitions des extrema locaux ou globaux et exemple 4.
- Condition nécessaire mais pas suffisante d'extremum local et logique : exo 23 p. 95.
- Faire l'exo 43 page 97, lire l'exo résolu 63 page 100 et faire l'exo 64 p. 100.
Séance du 20/03/2017
Chapitre 8 : Applications de la dérivation.
- Correction des 43 page 97 et 64 p. 100.
- Cours :
- Méthode pour étudier les variations d'une fonction dérivable, définitions des extrema locaux ou globaux : fin de l'exemple 4.
- Condition nécessaire mais pas suffisante d'extremum local : propriété et exemples 5 et 6 (variations d'une fonction rationnelle).
- Applications :
- Démontrer une inégalité : exemple 7.
- Etudier les variations par dérivations successives : exemple 8.
- Recherche de solution approchée d'équation par dichotomie : exercice 5 de la Fiche d'exercices . Certains corrigés d'exercices de cette fiche sont disponibles au format pdf ou html . Attention la numérotation des exos ne correspond pas.
- Finir l'exo 5 et faire l'exo 11 de la Fiche d'exercices .
- Rappel : le cours de 15 à 16 du mardi 21/03 est annulé et reporté au vendredi 24/03.
Séance du 21/03/2017
Chapitre 8 : Applications de la dérivation.
- Recherche de solution approchée d'équation par dichotomie : exercice 5 de la Fiche d'exercices . Certains corrigés d'exercices de cette fiche sont disponibles au format pdf ou html . Attention la numérotation des exos ne correspond pas.
- Cours :
- Applications :
- Démontrer une inégalité : exemple 7 (pas fini)
- Applications :
- Pour vendredi 24/03 : finir l'exemple 7 et faire les exos 3 et 7 de la Fiche d'exercices .
- Rappel : le cours de 15 à 16 du mardi 21/03 est annulé et reporté au vendredi 24/03.
- Pour le lundi 3/04 : DM n°9 avec fichier Algobox à télécharger.
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 24/03/2017
Chapitre 8 : Applications de la dérivation.
- Recherche de solution approchée d'équation par dichotomie : exercice 5 de la Fiche d'exercices . Certains corrigés d'exercices de cette fiche sont disponibles au format pdf ou html . Attention la numérotation des exos ne correspond pas.
- Voici un programme de recherche dichotomique pour calculatrice TI 83 Premium.
- Cours :
- Applications :
- Démontrer une inégalité : exemple 7 (correction)
- Applications :
- Correction des exos 7 et 11 de la Fiche d'exercices .
Chapitre 9 : Suites, sens de variation et notion de limites.
- Cours : 1. Sens de variation d'une suite
- Définition .
- Pour le lundi 27/03 : TP Dichotomie en salles 715 et 716.
- Pour le mardi 280/3 : exercices 16 à 20 page 125 (sur le sens de variation d'une suite).
- Pour le lundi 3/04 : DM n°9 avec fichier Algobox à télécharger.
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 27/03/2017
TP Balayage et Dichotomie en salles 715 et 716.
- Un corrige du TP
- Voici un programme de recherche dichotomique pour calculatrice TI 83 Premium.
AP
- Variables aléatoires, répétition d'expériences identiques et indépendantes : exo 64 p. 285 et Activité 1 page 296.
- Suites : exercice 6 (suite arithmético-géométrique et algorithme de seuil ) de la Fiche n°3 sur les Suites. (pas terminé)
- Pour le mardi 28/03 : l'exo 6 de la Fiche n°3 sur les Suites. et faire les exos exercices 16 à 20 page 125 (sur le sens de variation d'une suite).
- Pour le lundi 3/04 : DM n°9 avec fichier Algobox à télécharger.
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 28/03/2017
Chapitre 9 : Suites, sens de variation et notion de limites.
- Correction d'exercices sur les suites : exercice 6 (suite arithmético-géométrique et algorithme de seuil ) de la Fiche n°3 sur les Suites. et exercices 16 à 20 page 125 (sur le sens de variation d'une suite).
- Cours : 1. Sens de variation d'une suite
- Définition .
- Exemple 1 :
- Méthode 1 : étude du signe de \(u_{n+1}-u_{n}\)
- Méthode 2 : comparer \( \frac{u_{n+1}}{u_{n}} \) et 1.
- Pour le jeudi 30/03 : finir l'exemple 1 (Méthode 2 a) et Méthode 3 a) ) du cours et faire l'exemple 2
- Pour le lundi 3/04 : DM n°9 avec fichier Algobox à télécharger.
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 30/03/2017
Chapitre 9 : Suites, sens de variation et notion de limites.
- Correction d'exercices sur les suites : exercice 6 (suite arithmético-géométrique et algorithme de seuil ) de la Fiche n°3 sur les Suites. et exercices 16 à 20 page 125 (sur le sens de variation d'une suite).
- Cours : 1. Sens de variation d'une suite
- Définition .
- Exemple 1 :
- Méthode 2 : comparer \( \frac{u_{n+1}}{u_{n}} \) et 1, fin.
- Méthode 3 : si \( u_{n} = f(n) \) on peut étudier les variations de \(f\) en la dérivant.
- Sens de variation d'une suite arithmétique ou géométrique : propriétés et exemple 2.
- Pour le lundi 3/04 : DM n°9 avec fichier Algobox à télécharger.
- Pour le mardi 4/04 :préparer l'exemple 4 (conjecture sur le comportement asymptotique d'une suite avec la calculatrice, convergence et terminaison de boucle) du Chapitre 9 : Suites, sens de variation et notion de limites. .
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 04/04/2017
Chapitre 9 : Suites, sens de variation et notion de limites.
- Récolte du DM n°9 .
- Cours : 2. Comportement asymptotique d'une suite
- Exemple 2 : suite arithmético-géométrique
- Définition d'une suite convergente.
- Exemple 4 : conjectures sur le comportement asymptotique d'une suite avec la calculatrice et arrêt de boucle.
- Propriété de limite des suites géométriques.
-
Soit une suite \((u_{n})\) strictement décroissante et \(f\) une fonction strictement croissante sur \(\mathbb{R}\).
Que peut-on dire du sens de variation de la suite \((u_{n})\) définie pour tout entier \( n \geqslant 0 \) par \( v_{n} = f(u_{n}) \).
- Pour le mardi 11/04 : préparer l'exemple 5 du cours et faire l'exo 5 de la Fiche n°3 sur les Suites. .
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 06/04/2017
Chapitre 9 : Suites, sens de variation et notion de limites.
- Cours : 2. Comportement asymptotique d'une suite
- Définition d'une suite divergente et d'une suite tendant vers \(+ \infty \) ou \(-\infty \).
- Exemple 5 : VRAI/FAUX sur les limites de suites.
- Pour le lundi 10/04 : exercices d'entrainement sur le sens de variation ou la limite d'une suite : exercices 62 et 63 p. 128, 55 p. 127.
- Prochain DS de 2 heures : le lundi 10/04.
Séance du 10/04/2017
DS n° 9 sur Variables aléatoires, Applications de la dérivation, Dichotomie et Sens de variation et limites de suites
Chapitre 10 : Angles et trigonométrie.
- 1 Cercle trigonométrique et radian : 1.1 Repérage sur le cercle trigonométrique, définitions, propriétés 1 et 2 et exemple 1
- Pour le mardi 10/04 : préparer les exemples 2 et 3 du cours .
- Pour le mardi 02/05 : DM n° 10
- Pas de cours le mardi 2/05 au matin, le cours est rattrapé le vendredi 17/04 de 16 à 17 en 822.
Séance du 11/04/2017
Chapitre 10 : Angles et trigonométrie.
- 1.2 Mesure en radians d'un angle géométrique : définition, propriété 3 et exemple 2
- 2. Mesure d'un angle orienté : définition, propriété 4 mesure principale, méthodes pour déterminer une mesure principale et exemple 3.
- Pour le jeudi 13/04 : faire les exos 71,72 et 75 p. 180.
- Pour le mardi 02/05 : DM n° 10
- Pas de cours le mardi 2/05 au matin, le cours est rattrapé le vendredi 14/04 de 16 à 17 en 822.
Séance du 13/04/2017
Chapitre 10 : Angles et trigonométrie.
- Caractérisation de la colinéarité et de l'orthogonalité, relation de Chasles et exemple 4.
- Pour le vendredi 14/04 : propriétés des angles orientés : exos 64, 65 et 66 p. 180 .
- Pour le mardi 02/05 : DM n° 10
Séance du 14/04/2017
Chapitre 10 : Angles et trigonométrie.
- 3. Cosinus et sinus : définition, valeurs remarquables.
- Propriétés de symétrie de cosinus et sinus + exemple 5.
- Équations trigonométriques : méthodes et exemple 6.
- Pour le mardi 02/05 : DM n° 10
Pâques
Séance du 02/05/2017
Chapitre 10 : Angles et trigonométrie.
- Corrigé des exemples du cours
- Récolte du DM n° 10
- Retour du DS n°9.
- Cours :
- 3. Cosinus et sinus : définition, valeurs remarquables.
- Propriétés de symétrie de cosinus et sinus.
- Exercices :
- Cosinus et sinus des angles associés : exercices 28 à 32 p. 177.
- Corrigé d'exercices du manuel
- Pour le vendredi 05/05 :
- Cosinus et sinus des angles associés : faire les exos 29 à 32 page 177, l'exemple 5 du cours et les exos .
- Cosinus et sinus des angles associés : exercices 29 à 32 p. 177.
- Pour le lundi 15/05 : DS d'une heure sur le chapitre Chapitre 10 : Angles et trigonométrie. .
Séance du 05/05/2017
Chapitre 10 : Angles et trigonométrie.
- Corrigé des exemples du cours
- Correction d'exercices : Cosinus et sinus des angles associés : exos 29 à 32 page 177 puis lignes trigonométriques : exercices 29 à 32 p. 177.
- Cours :
- Propriétés de symétrie de cosinus et sinus : correction de l'exemple 5.
- Cours : équations et inéquations trigonométriques : méthode et exemple 6 (pas terminé).
- Corrigé d'exercices du manuel
- Pour le mardi 09/05 :
- Equations trigonométriques : finir l'exemple 6 et faire les exos 101,104 et 105 page 182.
- Exercice dicté :
- Résoudre dans \(\mathbb{R}\) l'équation \( 2X^2+X-1 =0 \)
- En posant \(X = \cos x\), en déduire la résolution dans l'intervalle \(]-\pi; \pi] \) de l'équation \(2 (\cos x )^2 + \cos x - 1 = 0 \)
- Pour le lundi 15/05 : DS d'une heure sur le chapitre Chapitre 10 : Angles et trigonométrie. .
Séance du 09/05/2017
Chapitre 10 : Angles et trigonométrie.
- Corrigé des exemples du cours
- Cours : équations trigonométriques : fin de l'exemple 6.
- Correction d'exercices sur les équations trigonométriques :
- Exercice dicté :
- Résoudre dans \(\mathbb{R}\) l'équation \( 2X^2+X-1 =0 \)
- En posant \(X = \cos x\), en déduire la résolution dans l'intervalle \(]-\pi; \pi] \) de l'équation \(2 (\cos x )^2 + \cos x - 1 = 0 \)
- Exercice dicté :
- Cours : inéquations trigonométriques : exemple 7.
- Corrigé d'exercices du manuel
Chapitre 11 : Produit scalaire et applications.
- Cours sur le produit scalaire :
- Définition (avec les carrés scalaires) et expression analytique :
- Définition 1, propriété 1 et exemple 1
- Définition 2 et propriété 2 : orthogonalité de 2 vecteurs et caractérisation (théorème de Pythagore).
- Définition (avec les carrés scalaires) et expression analytique :
- Pour le jeudi 10/05 :
- Angles et trigonométrie : exos 124, 125, 126 page 183.
- Pour le lundi 15/05 : DS d'une heure sur le chapitre Chapitre 10 : Angles et trigonométrie. .
Séance du 11/05/2017
Chapitre 11 : Produit scalaire et applications.
- Cours sur le produit scalaire :
- Définition (avec les carrés scalaires) et expression analytique :
- Fin de l'exemple 1
- Expression analytique du produit scalaire (avec preuve ROC)
- Définition (avec les carrés scalaires) et expression analytique :
- Exercices sur le produit scalaire : exos 8,14,15 page 202.
- Pour le vendredi 12/05 :
- Produit scalaire : exos 17,18 page 202.
- Pour le lundi 15/05 : DS d'une heure sur le chapitre Chapitre 10 : Angles et trigonométrie. .
Séance du 12/05/2017
Chapitre 11 : Produit scalaire et applications.
- Applications de l'expression analytique du produit scalaire : correction des exos 17 et 18 page 202.
- Cours sur le produit scalaire :
- Expression analytique : application et algorithmique avec l'exemple 2 1) .
- Propriétés algébriques : bilinéarité (P4) et produit scalaire de vecteurs colinéaires (P5) et exemple 3.
- Projection orthogonale : propriété 6.
- Exercices sur les propriétés de bilinéarité et de projection orthogonale du produit scalaire : exo 23 page 203 (pas terminé).
- Pour le lundi 15/05 : DS d'une heure sur le chapitre Chapitre 10 : Angles et trigonométrie. .
- Pour le mardi 23/05 : DM n° 11, faire sur feuille les exercices 51 page 229, 67 page 230, 104 et 105 page 233.
Séance du 15/05/2017
DS n° 10 sur le chapitre Chapitre 10 : Angles et trigonométrie.
Chapitre 11 : Produit scalaire et applications.
- Exercices sur les propriétés de bilinéarité et de projection orthogonale du produit scalaire : exos 20, 23 et 24 page 203 .
- Lire la preuve du théorème de la médiane p 200 et faire l'exo 35 page 203.
- Pour le mardi 23/05 : DM n° 11, faire sur feuille les exercices 51 page 229, 67 page 230, 104 et 105 page 233.
Séance du 16/05/2017
Chapitre 11 : Produit scalaire et applications.
- Cours :
- Théorème du cosinus et exemple 6.
- Théorème de la médiane avec preuve ROC.
- Théorème d'Al KAshi (preuve ROC) et exemple 8.
- Applications du produit scalaire aux équations de droites : définition et propriétés d'un vecteur normal + exemple 9, .
- Quelques corrigés des exemples du cours et ou des exercices de la fiche d'exercices.
- Pour le vendredi 19/05 : finir l'exemple 9.
- Pour le mardi 23/05 : DM n° 11, faire sur feuille les exercices 50 et 51 page 229, puis 104 page 233, et 73 et 86 page 231.
Séance du 19/05/2017
Chapitre 11 : Produit scalaire et applications.
- Cours :
- Applications du produit scalaire aux équations de droites : définition et propriétés d'un vecteur normal + exemple 9 (correction) , théorème (équation cartésienne d'une droite avec vecteur normal), propriété 8 (caractérisation du parallélisme et de l'orthogonalité).
- Exercices sur les équations de droites avec vecteur normal : exercices 35 (droite avec point et vecteur normal),37 (perpendiculaire),38 (hauteur),40 (médiatrice) page 228
- Quelques corrigés des exemples du cours et ou des exercices de la fiche d'exercices.
- Pour le mardi 23/05 : DM n° 11, faire sur feuille les exercices 50 et 51 page 229, puis 104 page 233, et 73 et 86 page 231.
Séance du 22/05/2017
Chapitre 11 : Produit scalaire et applications.
- Cours :
- Applications du produit scalaire aux équations de droites : théorème (équation cartésienne d'une droite avec vecteur normal) avec preuve de ROC et propriété 8 (caractérisation du parallélisme et de l'orthogonalité) puis exemple 10 (équations de hauteur, de médiatrice).
- Applications du produit scalaire aux équations de cercles : théorèmes 5 et 6.
- Applications du produit scalaire à la trigonométrie : Propriété 9 (formules d'addition).
- Exercices sur les applications du produit scalaire :
- Equations de cercle et de droites : exos 12, 13, 14, 15 et 17 page 227 et exo 67 page 230.
- Formule d'addition et de duplication : exo 28 page 227.
- Quelques corrigés des exemples du cours et ou des exercices de la fiche d'exercices.
- Pour le mardi 23/05 : DM n° 11, faire sur feuille les exercices 50 et 51 page 229, puis 104 page 233 et 73 et 86 page 231.
Séance du 23/05/2017
Chapitre 11 : Produit scalaire et applications.
- Récolte du DM n° 11.
- Exercices sur les formules d'addition : exos 28,29,32,33 page 227.
- Cours :
- Applications du produit scalaire à la trigonométrie : Propriété10 (formules de duplication) et exemple 12.
- Quelques corrigés des exemples du cours et ou des exercices de la fiche d'exercices.
Chapitre 11 : Loi binomiale et échantillonnage.
- Cours :
- 1 Loi de Bernoulli et schéma de Bernoulli : définition et exemples 1, 2, 3.
- Pour le lundi 29/05 :
- Finir l'exemple 3 du cours.
- Exercices sur le schéma de Bernoulli : exos 2 et 4 p. 306.
- Exercices sur la loi binomiale : exos 7 et 11 page 306.
Séance du 29/05/2017
Chapitre 11 : Loi binomiale et échantillonnage.
- Correction des exos 2,4,7,11 page 306.
- Cours :
- 1 Loi de Bernoulli et schéma de Bernoulli : exemple 3.
-
Cours :
- 2 Loi binomiale, définition et propriétés de la loi binomiale : \(\mathbb{P}(X=0) \), \(\mathbb{P}(X=1) \), \(\mathbb{P}(X=n) \), \(\mathbb{P}(X=n-1) \); \(\mathbb{E}(X) \) : exemple 5.
- Pour le mardi 30/05 :
- Lire la définition 4 du cours sur les coefficients binomiaux et faire les exos 12,13,14,15 et 18 p. 307.
Séance du 30/05/2017
Chapitre 11 : Loi binomiale et échantillonnage.
-
Cours :
- 3 Coefficients binomiaux : définition et exemples 6 et 7.
- 3 Coefficients binomiaux : relation de Pascal, exemple 8 et propriété 4.
- Cours :
- 3 Coefficients binomiaux et loi binomiale : exemple 9 (utilisation de la calculatrice, formulation d'événements sous la forme \( X = k \), \( X \leqslant k \) ou \( X \geqslant k \) ).
- Présentation des spécialités Mathématiques et ISN
- Pour le vendredi 02/06 : faire les exercices 51, 52 et 53 page 311.
Séance du 02/06/2017
Chapitre 11 : Loi binomiale et échantillonnage.
- Calculs de probabilités pour la loi binomiale avec la calculatrice : correction des exercices 51, 52 et 53 page 311.
- Cours :
- Espérance de la loi binomiale : propriété et exemple 10.
- Intervalle de fluctuation et prise de décision : exemple 13
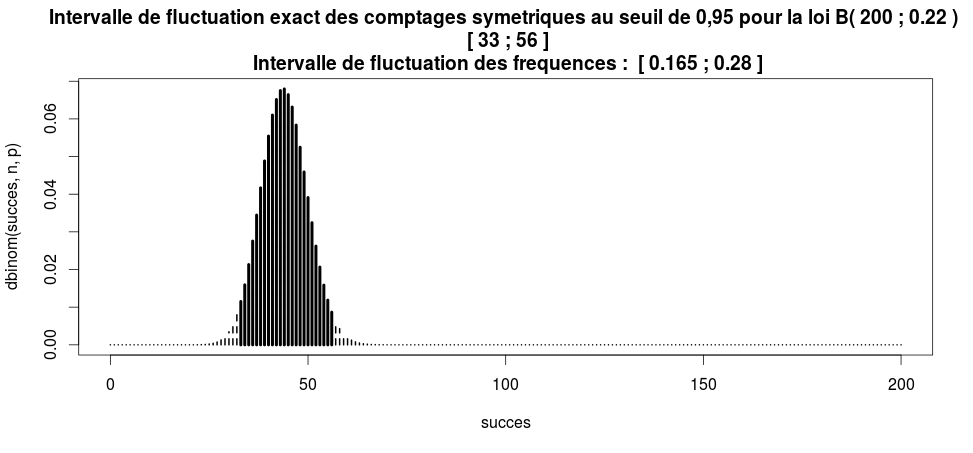
- Présentation des spécialités Mathématiques et ISN
Séance du 06/06/2017
Chapitre 11 : Loi binomiale et échantillonnage.
- Cours, voir aussi mon diaporama sur l'intervalle de fluctuation exact.
- Intervalle de fluctuation exact au seuil de 95 % : introduction avec l'exemple 11 puis méthode pour le déterminer.
- Intervalle de fluctuation exact au seuil de 95 % : algorithme pour le déterminer et programmatio nde l'algorithme avec l'exemple 12.
- Intervalle de fluctuation et prise de décision : exemple 13

- Exercices de la fiche sur la loi binomiale et l'échantillonnage.
- Présentation des spécialités Mathématiques et ISN