Continuité, corrigés des exemples du cours

Pdf du Cours, mot de passe : parcTerminale

Capacité 1

capacité 1

La fonction représentée ci-dessous est définie mais discontinue en 0 car .

Capacité 1

Une fonction définie sur telle que et et ne s'annule pas sur , ne peut être continue sur .

Capacité 2

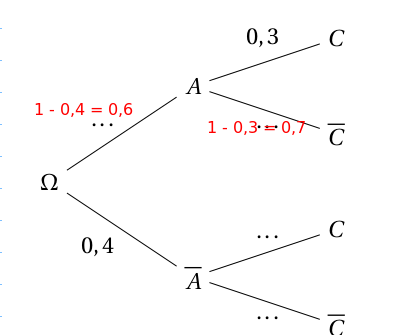
Dans un pays X, on note le nombre, exprimé en millions, de foyers possédant une voiture sans conducteur en l'année .

On a et pour tout entier , .

Capacité 2

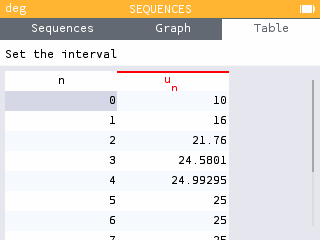
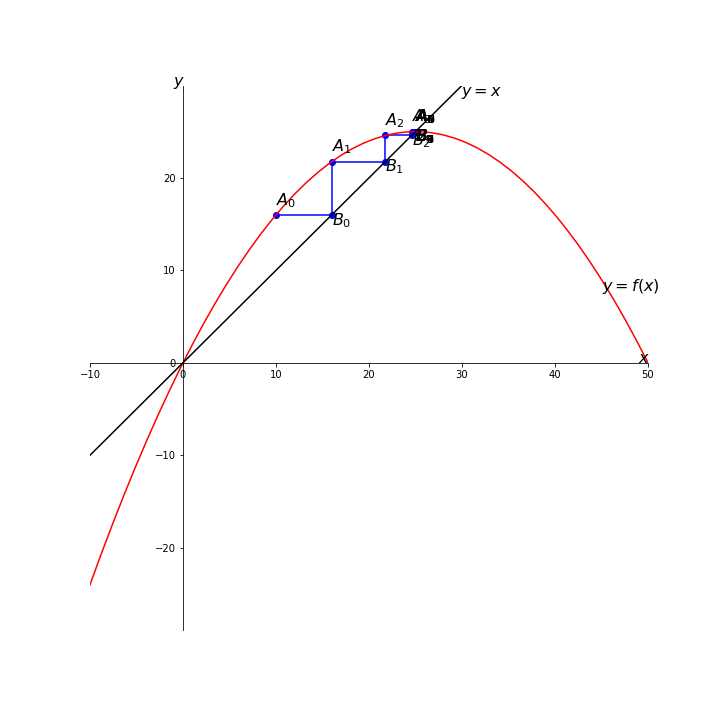
Représentation des quatre premiers termes ci-dessous.

capacite 2

Capacité 2

def autonome(n):
	u = 10
    for k in range(n):
        u = 0.04 * u * (50 - u)
    return u

On peut conjecturer que la suite converge vers .

capacite 2

Capacité 2

  • La fonction définie sur par est continue car dérivable sur .
  • Si on admet que la suite converge vers une limite alors d'après une propriété du cours :

En passant à la limite dans l'égalité :

Il vient :

En résolvant cette équation du second degré, on trouve deux solutions ou . Mais on admet que la suite est croissante et , donc .

Capacité 3

Soit la fonction dérivable sur définie par .

  • Démontrons que s'annule sur :
    • D'une part, est dérivable donc continue sur .
    • D'autre part, et , donc on a .
    • Donc d'après le théorème des valeurs intermédiaires, l'équation possède au moins une solution dans .

Capacité 3

Soit la fonction dérivable sur définie par .

  • Démontrons que posède au moins une solution sur :
    • D'une part, est dérivable donc continue sur .
    • D'autre part, et , donc on a .
    • Donc d'après le théorème des valeurs intermédiaires, l'équation possède au moins une solution dans .

Capacité 4

capacite4

Capacité 4

  • est dérivable donc continue sur .
  • et , donc on a
  • est strictement croissante sur
  • Donc d'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle
  • De plus le minimum de sur est donc n'a pas d'autre solution sur

Capacité 4

  • est dérivable donc continue sur .
  • et , donc on a
  • est strictement croissante sur
  • D'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle
  • mutatis mutandis on démontre que l'équation possède une unique solution sur et une unique solution sur .

Capacité 4

  • Le minimum de sur est donc l'équation n'a pas de solution sur .

Capacité 4

  • Le minimum de sur est donc l'équation n'a pas de solution sur .
  • est dérivable donc continue sur .
  • et , donc on a
  • est strictement croissante sur
  • D'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle

Capacité 5

Soit la fonction définie sur par .

  • est dérivable sur et pour tout réel :

  • D'après la règle du signe d'un trinôme :
    • et strictement croissante sur
    • et strictement décroissante sur

Capacité 5

  • est dérivable donc continue sur .
  • et , donc on a
  • est strictement croissante sur
  • Donc d'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle

Capacité 5

  • est dérivable donc continue sur .
  • et , donc on a
  • est strictement décroissante sur
  • Donc d'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle .

Capacité 5

  • est dérivable donc continue sur .
  • et
  • est strictement décroissante sur
  • Donc d'après un corollaire du théorème des valeurs intermédiaires, l'équation possède une unique solution dans l'intervalle

Capacité 5

Considérons l'unique solution de dans .

On a donc .

De plus est strictement croissante sur , donc .

Capacité 5

Approximation de par balayage sachant que est strictement croissante sur .

def f(x):
	return x ** 3 - 6 * x ** 2 + 6
	
def balayage():
	x = 5
	while f(x) < 0>:
		x = x + 0.1
	return (x - 0.1, x)

Capacité 5

On peut déduire du tableau de variations de que :

  • est négative sur
  • s'annule en
  • est positive sur
  • s'annule en
  • est négative sur
  • s'annule en
  • est positive sur