Limite de suite capacité 2

Question 1

Soit la suite $u$ définie pour tout entier $n \geqslant 1$ par :

$u_{n}=\sqrt{n}$

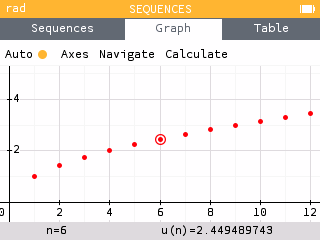
On conjecture que $u$ a pour limite $+\infty$.

Question 1 partie 1

Soit désormais un réel $a>0$ quelconque

$u_{n}>a$
$\Longleftrightarrow \sqrt{n} > a$
$\Longleftrightarrow n > a^{2}$

Question 1

Pour tout réel $a>0$, il existe un entier $n_{a}$ qui est
le plus petit entier supérieur à $a^{2}$ tel que :

$\forall n \geqslant n_{a}, u_{n}>a$

Par définition, la suite $u$ a pour limite $+\infty$.

On note $\lim\limits_{n \to +\infty}u_{n}=+\infty$

Question 2 a)

On considère l'algorithme :

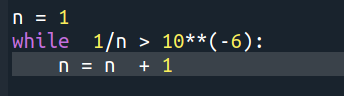
L'algorithme se termine car $\lim\limits_{n \to +\infty} \frac{1}{n}=0$ donc il existe un entier $n_{a}$ tel que :

$\vert \frac{1}{n} \vert \leqslant 10^{-6} \Longleftrightarrow -10^{-6} \leqslant \frac{1}{n} \leqslant 10^{-6}$.

Question 2 b)

On considère l'algorithme :

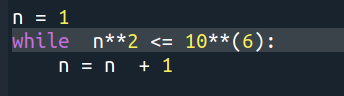
L'algorithme se termine car

$\lim\limits_{n \to +\infty}n^{2}=+\infty$ donc il existe un entier $n_{a}$ tel que : $n^{2} > 10^{6}=a$