Limite de suite capacité 1

Question 1

Soit la suite uu définie pour tout entier n⩾1n \geqslant 1 par :

un=1−1nu_{n}=1-\frac{1}{n}

Question 1 a)

Pour tout entier n⩾1n\geqslant 1 :

un+1−un=−1n+1+1n=−n+n+1n(n+1)u_{n+1}-u_{n}=-\frac{1}{n+1}+\frac{1}{n}=\frac{-n+n+1}{n(n+1)}

donc un+1−un>0u_{n+1}-u_{n}>0

donc uu est croissante.

Question 1 b)

alt

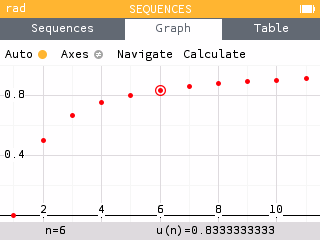
On conjecture que uu converge vers 11.

Question 1 c)

un∈]1−10−3;1+10−3[u_{n} \in ]1 - 10^{-3};1+10^{-3}[
⟺∣un−1∣<10−3\Longleftrightarrow \vert u_{n} -1 \vert < 10^{-3}
⟺∣−1n∣<10−3\Longleftrightarrow \vert -\frac{1}{n} \vert < 10^{-3}
⟺1n<10−3\Longleftrightarrow \frac{1}{n} < 10^{-3} car 1n>0\frac{1}{n}>0
⟺n>10+3\Longleftrightarrow n > 10^{+3}

Donc un∈]1−10−3;1+10−3[u_{n} \in ]1 - 10^{-3};1+10^{-3}[ à partir de n=103+1n=10^{3}+1

Question 1 d) partie 1

Soit désormais un réel a>0a>0 quelconque, on raisonne comme pour a=10−3a=10^{-3}.

∣un−1∣<a\vert u_{n} -1 \vert < a
⟺∣−1n∣<a\Longleftrightarrow \vert -\frac{1}{n} \vert <a
⟺1n<a\Longleftrightarrow \frac{1}{n} < a
⟺n>1a\Longleftrightarrow n > \frac{1}{a}

Question 1 d) partie 2

Pour tout réel a>0a>0, il existe un entier nan_{a} qui est
le plus petit entier supérieur à 1a\frac{1}{a} tel que :

∀n⩾na,∣un−1∣<a\forall n \geqslant n_{a}, \vert u_{n} -1 \vert < a

Par définition, la suite uu converge vers 11.

On note lim⁡n→+∞un=1\lim\limits_{n \to +\infty}u_{n}=1

Question 2

Soit la suite vv définie pour tout entier n⩾1n \geqslant 1 par :

vn=1−(−1)nnv_{n}=1-\frac{(-1)^{n}}{n}

Question 2 a)

On a v1=1+1=2v_{1}=1+1=2, v2=1−12=12v_{2}=1-\frac{1}{2}=\frac{1}{2} et v3=1−−13=43v_{3}= 1 - \frac{-1}{3}=\frac{4}{3}

Question 2 b)

alt

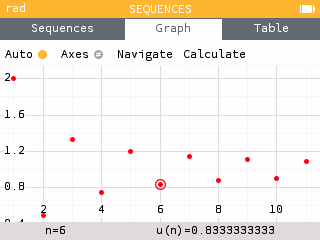
On conjecture que vv converge vers 11.

Question 2 c)

Soit désormais un réel a>0a>0 quelconque, on raisonne comme pour la suite uu.

∣vn−1∣<a\vert v_{n} -1 \vert < a
⟺∣−(−1)nn∣<a\Longleftrightarrow \vert -\frac{(-1)^{n}}{n} \vert <a
⟺1n<a\Longleftrightarrow \frac{1}{n} < a
⟺n>1a\Longleftrightarrow n > \frac{1}{a}

Question 1 d) partie 2

Pour tout réel a>0a>0, il existe un entier nan_{a} qui est
le plus petit entier supérieur à 1a\frac{1}{a} tel que :

∀n⩾na,∣vn−1∣<a\forall n \geqslant n_{a}, \vert v_{n} -1 \vert < a

Par définition, la suite vv converge vers 11.

On note lim⁡n→+∞vn=1\lim\limits_{n \to +\infty}v_{n}=1

Remarque

Dans cet exercice on a rencontré une suite croissante uu et une suite non monotone vv qui convergent vers la même limite.

Les notions de sens de variation et de limite sont donc bien distinctes, même si on verra un lien entre les deux avec le théorème de convergence monotone.