Méthode d'Euler

Définition de la fonction exponentielle

On admet qu'il existe une unique fonction $f$ dérivable sur $\R$ telle que :

$\begin{cases} f' = f \\ f(0)=1 \end{cases}$

C'est une équation différentielle avec conditions initiales.

Preuve de l'existence ?

Dans le chapitre intégration, on jutifiera l'existence de la fonction $\ln$ comme primitive de la fonction inverse.

Preuve de l'unicité ?

Faisable dès le niveau première.

Calculer des valeurs ?

Avec des additions et des multiplications on ne peut calculer que des approximations par la méthode d'Euler

Approximation affine

$f(a+h) \approx f'(a) \times h + f(a)$

On approche la courbe par sa tangente.

Approximation affine

Et on itère le procédé :

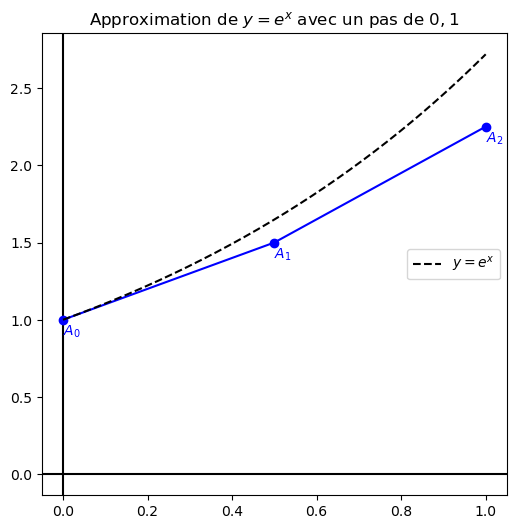
Approximation affine

Et on itère encore. Plus les pas sont petits mieux on approchera la valeur de l'exponentielle qu'on souhaite approcher :

Un peu de calcul

Notre objectif : une valeur approchée de $f(1)$, calculée uniquement avec les opérations arithmétiques de base.

Un peu de calcul

On fixe le nombre d'itérations (ou pas), disons 10.
On va calculer $y_{0}$ valeur approchée de $f(0)$, $y_{1}$ valeur approchée de $f(0,1)$,
$y_{2}$ valeur approchée de $f(0,2)$, ... , $y_{10}$ valeur approchée de $f(10 \times 0,1)$.

Un peu de calcul

On commence avec une valeur exacte :

$y_{0}=f(0)$

Pour $y_{1}$ on prend l'approximation affine :

$y_{1} \approx f(0,1) \approx f(0) + 0,1 \times f'(0)$.

Or $f'=f$ et $f(0)=1=y_{0}$ donc :

$y_{1} \approx y_{0} \times 1,1$.

Un peu de calcul

Pour $y_{2}$, on reprend une approximation affine

$y_{2} \approx f(0,2)$ avec :

$f(0,2) \approx f(0,1) + 0,1 \times f'(0,1)$.

or $f'(0,1)=f(0,1)$

donc $y_{2} \approx f(0,2) \approx f(0,1)\times 1,1$

Un peu de calcul

On ne connaît pas $f(0,1)$

mais $y_{1} \approx f(0,1)$ donc

$y_{2} = y_{1} \times 1,1 = y_{0} \times 1,1^{2}$.

Un peu de calcul

On réitère :

$y_{3} = y_{2} \times 1,1 = y_{0} \times 1,1^{3}$

$y_{k+1} = y_{k} \times 1,1 = y_{0} \times 1,1^{k}$

$y_{10} = y_{9} \times 1,1 = y_{0} \times 1,1^{10}$

La suite $y$ est géométrique.

Un peu de calcul

Avec la méthode d'Euler on a obtenu l'approximation de l'exponentielle de 1 :

$f(1)=\text{e}^{1} \approx 1,1^{10}$

>>> 1.1**10
2.5937424601000023
>>> from math import exp
>>> exp(1)
2.718281828459045

Courbe approchée de l'exponentielle

Augmentons le nombre d'itérations

Si on augmente le nombre d'itérations pour approcher $f(1)$, on diminue la taille des pas et l'approximation est améliorée.

On généralise la méthode d'Euler pour approcher $f(1)$ depuis la valeur exacte $f(0)=y_{0}$ avec $n$ pas.

Augmentons le nombre d'itérations

Avec les approximations affines :

$f((k+1) \times 1/n) \approx f(k \times 1/n) + 1/n \times f'(k \times 1/n)$

Où $f(k \times 1/n) \approx y_{k}$

et $f'(k \times 1/n)=f(k / n) \approx y_{k}$

Augmentons le nombre d'itérations

donc

$f((k+1) \times 1/n) \approx y_{k} \times (1+1/n)$

et $y_{k+1} \approx y_{k} \times (1+1/n)$

Augmentons le nombre d'itérations

La suite $y$ est géométrique de raison $1/n$

On a $f(1) \approx y_{n} = y_{0} \times (1 + 1/n)^{n}$.

On approche $f(1)$ par $(1 + 1/n)^{n}$, terme d'une suite géométrique.

>>> (1+1/5)**5
2.4883199999999994
>>> (1+1/10)**10
2.5937424601000023
>>> (1+1/50)**50
2.691588029073608
>>> (1+1/100)**100
2.7048138294215285
>>> from math import exp
>>> exp(1)
2.718281828459045

Conclusion

La méthode d'Euler est une méthode numérique qui permet d'approcher la solution de l'équation différentielle $f'=f$ telle que $f(0)=1$.

Nous verrons dans le chapitre un théorème permettant de résoudre de façon exacte des équations différentielles du même type.