Exemple 1

1. Sur TI, l'instruction pour simuler une naissance Fille (codée 0) ou Garçon (codé 1) est nbreAléatEnt(0, 1).

   Sur TI, l'instruction pour simuler une famille de 4 enfants est nbreAléatEnt(0, 1, 4).

   Pour simuler un échantillon de 10 familles de 4 enfants on répète dix fois cette instruction.

2. Arbre de dénombrement d'une famille de 4 enfants.

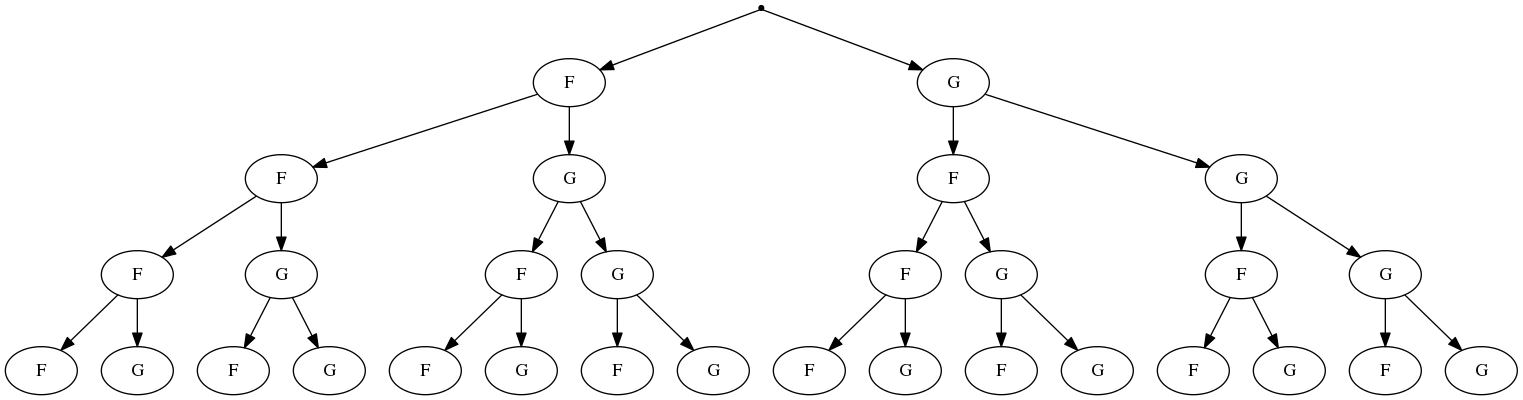
Arbre de dénombrement

3. Sur l'univers des 16 filles possibles en tenant compte de l'ordre des naissances et du sexe, on définit une loi de probabilité en associant à chaque issue élémentaire (une des 16 familles), une probabilité de \(\frac{1}{16}\). Il s'agit d'une loi d'équiprobabilité car toutes les issues élémentaires ont la même probabilité.

   Ainsi la somme des probabilités de toutes les issues élémentaires est \(\frac{16}{16}=1\).

   On peut alors calculer les probabilités de certains événements deux à deux disjoints et formant une partition de l'univers.

   • La probabilité d'avoir 0 fille dans une famille de 4 enfants est \(\frac{1}{16}\).

   • La probabilité d'avoir 1 fille dans une famille de 4 enfants est \(\frac{4}{16}\).

   • La probabilité d'avoir 2 filles dans une famille de 4 enfants est \(\frac{6}{16}\).

   • La probabilité d'avoir 3 filles dans une famille de 4 enfants est \(\frac{4}{16}\).

   • La probabilité d'avoir 4 filles dans une famille de 4 enfants est \(\frac{1}{16}\).

Exemple 2

Un dé est truqué de façon que le six a 6 fois plus de chances de sortir que les cinq autres faces qui ont toutes la même chance d'apparaître. Calculer la probabilité d'apparition de chaque face puis la probabilité d'obtenir un nombre pair.

• Méthode 1

  On modélise cette expérience aléatoire avec un dé à 11 faces équilibré qui possède six faces numérotées 6 et cinq autres faces numérotées de 1 à 5

  La probabilité de la face 6 est donc de \(\frac{6}{11}\) et celles des autres numéros de face sont toutes égales à \(\frac{1}{11}\).

  On vérifie que la somme des probabilités de toutes les faces, qui forment une partition de l'univers, est \(\frac{6}{11} + 5 \times \frac{1}{11} = \frac{11}{11}=1\).

• Méthode 2

  L'univers de cette expérience aléatoire est \(\Omega = \{ 1,2,3,4,5,6 \}\).

  On note \(p_{i}\) la probabilité de la face portant le numéro \(i\) avec \(1 \leqslant i \leqslant 6\).

  On a \(p_{6}=6p_{1}\) et \(p_{1}= \cdots = p_{5}\).

  La somme des probabilités de toutes les issues élémentaires est égale à \(1\) c'est-à-dire \(p_{6}+5p_{1}=1\).

  En substituant \(p_{6}=6p_{1}\) à \(p_{6}\) on se ramène à la résolution de \(6p_{1}+5p_{1}=1 \Leftrightarrow p_{1}=\frac{1}{11}\).

  Puis on obtient \(p_{6}=\frac{6}{11}\). Il serait cependant plus rigoureux de résoudre un système d'équations par équivalences.

Exemple 4

1. Calculer la probabilité de trouver le podium d'une course de 8 athlètes de même niveau, en pronostiquant au hasard.

   On a \(8\) choix pour le premier.

   Puis \(7\) choix pour le second.

   Et enfin \(6\) choix pour le dernier.

   Soit un total de \(8 \times 7 \times 6 = 336\) podiums possibles en tenant compte de l'ordre.

   On a donc une probabilité de \(\frac{1}{336}\) de choisir le bon podium en en choisissant un au hasard.

2. 20 chevaux d'égale valeur sont alignés dans une course. Calculer la probabilité de trouver le bon quarté dans l'ordre en pariant au hasard.

   En raisonnant comme précédemment, on trouve qu'on a \(20 \times 19 \times 18 \times 17 = 116280\) quartés dans l'ordre.

   On a donc une probabilité de \(\frac{1}{116280}\) de choisir le bon podium en en choisissant un au hasard.

3. Calculer la probabilité de tirer successivement (sans remise) B,A,C dans une urne contenant A, B, C, D, E.

   On a \(5\) choix pour la première boule.

   Puis \(4\) choix pour la seconde boule.

   Et enfin \(3\) choix pour la dernière boule.

   Soit un total de \(5 \times 4 \times 3 = 60\) tirages possibles en tenant compte de l'ordre.

   On a donc une probabilité de \(\frac{1}{60}\) de tirer dans l'ordre les lettres B, A puis C.

   Comme il existe \(6 = 3 \times 2 \times 1\) de BAC, on a une probabilité de \(\frac{6}{60}=\frac{1}{10}\) de tirer les lettres B, A et C sans tenir compte de l'ordre.

4. Le code d'un cadenas est constitué de \(4\) chiffres entre \(0\) et \(9\), on compose un code au hasard, calculer la probabilité de composer :

   On a \(10^{4}\) codes possibles.

   • un code qui commence par \(50\) ;

     Il reste les deux derniers chiffres à choisir soit \(10 \times 10 = 10^{2}\) codes possibles commençant par \(50\).

     La probabilité de cet événement est donc de \(\frac{10^{2}}{10^{4}}= \frac{1}{10^{2}}\).

   • un code qui se termine par \(0\);

     Il reste les trois premiers chiffres à choisir soit \(10 \times 10 \times 10 = 10^{3}\) codes possibles se terminant par \(0\).

     La probabilité de cet événement est donc de \(\frac{10^{2}}{10^{4}}=\frac{1}{10}\).

   • un code qui comporte exactement trois \(9\) ;

     Supposons que la positions des trois \(9\) soit fixée, il reste alors \(9\) possibilités pour le dernier chiffre (différent de \(9\)).

     Par ailleurs la position des trois \(9\) est déterminée par celle du quatrième chiffre laissé libre et ce dernier peut se trouver en position 1,2,3 ou 4.

     Donc au total on a \(4 \times 9 = 36\) codes comportant trois \(9\).

     La probabilité de cet événement est donc de \(4 \times \frac{9}{10^{4}}\).

   • un code qui ne comporte aucun \(1\).

     Pour chacun des quatre chiffres du code, il nous reste \(9\) choix.

     On a donc \(9^4\) codes ne comportant aucun \(1\).

     La probabilité de cet événement est donc de \(\frac{9^{4}}{10^{4}}\).

Exemple 5

1. On a écrit sur les quatre faces d'un dé équilibré les lettres du mot ABBC.

   L'univers \(\Omega = \{ A, B,B, C \}\) de cette expérience aléatoire est constituée de \(4\) issues élémentaires équiprobables.

   1. La probabilité de l'événement "Lire un A" est \(\frac{1}{4}\).

      La probabilité de l'événement "Lire un B" est \(\frac{2}{4}=\frac{1}{2}\).

   2. On lance deux fois le dé ABBC (lancers indépendants).

   L'univers est constitué de \(4 \times 4= 16\) issues élémentaires qui sont des listes constituées des 2 lettres tirées dans l'ordre.

   Pour calculer la probabilité d'un événement E, il suffit de dénombrer les issues élémentaires avec l'arbre et d'appliquer la formule :

   \begin{equation*} \text{P}(\text{E})=\frac{\text{nombre d'issues qui réalisent E}}{\text{nombre total d'issues de } \Omega} \end{equation*}

   • la probabilité de lire le mot AB est \(\frac{2}{16}=\frac{1}{8}\)

     • la probabilité de lire le mot BC est \(\frac{2}{16}=\frac{1}{8}\)

     • la probabilité de lire un mot sans la lettre C est de \(\frac{3 \times 3}{16}= \frac{9}{16}\).

     • la probabilité de lire un mot avec au moins une fois la lettre C est \(1 - \frac{9}{16}=\frac{7}{16}\) car cet événement est le contraire du précédent.

2. Une classe de première comporte \(33\) élèves. \(15\) pratiquent le hand-ball (noté H), \(8\) le tennis (noté T) et \(17\) ne pratiquent ni l'un ni l'autre. On choisit un élève au hasard dans cette classe. Chaque élève a une probabilité de \(\frac{1}{33}\) d'être choisi.

• La probabilité qu'un élève choisi au hasard pratique les deux sports est \[ \mathbb{P}(T \cap H)=\frac{7}{33} \]

  • La probabilité qu'un élève choisi au hasard pratique au moins l'un des deux sports est \[ \mathbb{P}(T \cup H) = \mathbb{P}(T) + \mathbb{P}(H) - \mathbb{P}(T \cap H)=\frac{8}{33} + \frac{15}{33} - \frac{7}{33}= \frac{16}{33} \] ou encore \[ 1 - \mathbb{P}(\overline{T} \cap \overline{H}) = 1 - \frac{17}{33} = \frac{16}{33} \]