- La droite \(\mathcal{D}_{5}\) d'équation \(x=-3\) passe par les points de coordonnées \((-3,0)\) et \((-3,2)\). Elle est parallèle à l'axe des ordonnées.

Figure de l'exemple 1
F.Junier Lycée du Parc, Lyon
\(\mathcal{D}_{1}\) passe par les points \(C(0,-2)\) et \(D(1,2)\)
Coefficient directeur : \(m=\frac{y_{D}-y_{C}}{x_{C}-x_{D}}=\frac{2-(-2)}{1-0}=4\)
Ordonnée à l'origine : \(p=-2\)
Equation de \(D_{1}\) : \(y=4x-2\)
\(\mathcal{D}_{2}\) passe par les points \(E(0,6)\) et \(F(3,5)\)
Coefficient directeur : \(m=\frac{y_{F}-y_{E}}{x_{F}-x_{E}}=\frac{5-6}{3-0}=-\frac{1}{3}\)
Ordonnée à l'origine : \(p=6\)
Equation de \(D_{1}\) : \(y=-\frac{1}{3}x+6\)
\(\mathcal{D}_{3}\) passe par le points \(A(2,-1)\) et a pour coefficient directeur \(\frac{2}{3}\)
Coefficient directeur : \(m=\frac{2}{3}\)
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(-1=\frac{2}{3} \times 2 + p\) équivaut à \(p=-1 - \frac{4}{3}=-\frac{7}{3}\)
Equation de \(D_{3}\) : \(y=\frac{2}{3}x-\frac{7}{3}\)
\(\mathcal{D}_{4}\) d'équation \(y=\frac{3x-1}{2}\)
Soit \(B(-1,3/2)\), on a \(\frac{3x_{B}-1}{2}=-\frac{4}{2}=-2 \neq y_{B}\). Donc \(B\) n'appartient pas à la droite
Premier point de la droite \(\mathcal{D}_{4}\) : on fixe \(x=1\) et on calcule \(y=\frac{3 \times 1-1}{2}=1\). Le point de coordonnées \((1,1)\) appartient à \(\mathcal{D}_{4}\)
Second point de la droite \(\mathcal{D}_{4}\) : on fixe \(x=-1\) et on calcule \(y=\frac{3 \times (-1)-1}{2}=-2\). Le point de coordonnées \((-1,-2)\) appartient à \(\mathcal{D}_{4}\)

Figure de l'exemple 1
\(D_{1} : y = 5x - 2\) et \(D_{2} : y = 2x - 5\) ne sont pas parallèles (et sont donc sécantes) car leurs coefficients directeurs \(5\) et \(2\) sont différents.
\(D_{1} : y = -2 + 3x\) et \(D_{2} : y = -2 + 4x\) ne sont pas parallèles (et sont donc sécantes) car leurs coefficients directeurs \(3\) et \(4\) sont différents.
\(D_{1} : y = 0\) et \(D_{2} : y = 2\) sont parallèles car elles ont même coefficient directeur \(0\).
\(D_{1} : x = 0\) et \(D_{2} : x = 5\) sont parallèles car elles sont parallèles à l'axe des ordonnées.
\(D_{1} : y = -4 + 3x\) et \(D_{2} :y = \frac{6x-5}{2}\) sont parallèles car elles ont même coefficient directeur \(3=\frac{6}{2}\).
Ex1 Soit la droite d'ordonnée à l'origine \(4\) (et donc par \((0,4)\)) et passant par \(A(2,-1)\).
Ordonnée à l'origine : \(p=4\).
Coefficient directeur : \(m=\frac{4-(-1)}{0-2}=-\frac{5}{2}\) ou \(-1 = 2 \times m + 4 \Leftrightarrow m=-\frac{5}{2}\).
Equation de cette droite : \(y=-\frac{5}{2}x+4\).
Ex2 Soit la droite de coefficient directeur \(3\) et passant par \(A(-4,-2)\).
Coefficient directeur : \(m=3\).
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(-2 = 3 \times (-4) + p\) équivaut à \(12-2=10=p\).
Equation de cette droite : \(y=3x+10\).
Ex3 \(A(-5,1)\) et \(B(6,5)\)
\(x_{B} \neq x_{A}\) donc la droite \((AB)\) n'est pas parallèle à l'axe des ordonnées et possède une équation du type \(y=mx+p\).
Coefficient directeur : \(m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{5-1}{6-(-5)}=\frac{4}{11}\).
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(1= -5 \times \frac{4}{11} + p\) équivaut à \(\frac{31}{11}=p\).
Equation de cette droite : \(y=\frac{4}{11}x+\frac{31}{11}\).
Ex4 \(A(2,-1)\) et \(B(6,-1)\)
\(x_{B} \neq x_{A}\) donc la droite \((AB)\) n'est pas parallèle à l'axe des ordonnées et possède une équation du type \(y=mx+p\).
Coefficient directeur : \(m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{-1-(-1)}{6-2}=0\).
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(-1= p\).
Equation de cette droite : \(y=-1\).
On remarque que si \(x_{B} \neq x_{A}\) et \(y_{B}= y_{A}\) alors la droite \((AB)\) est parallèle à l'axe des abscisses et son équation est \(y=y_{A}\).
Ex5 \(A(5,-3)\) et \(B(5,2)\)
\(x_{B} = x_{A}\) donc la droite \((AB)\) est parallèle à l'axe des ordonnées et possède une équation du type \(x = k\).
\(A\) appartient à la droite \((AB)\) : \(x_{A}=k\) équivaut à \(5 =k\).
Equation de cette droite : \(x=5\).
Ex6 Dans un repère (O, I, J), \(\mathcal{D}\) est la droite d'équation \(y= \frac{1}{3}x-2\).
Equation de la droite \(\mathcal{D}_{1}\) passant par \(A(1,2)\) et parallèle à \(\mathcal{D}\) :
Coefficient directeur : il est égal à \(\frac{1}{3}\), celui de \(\mathcal{D}\) car \(\mathcal{D}\) et \(\mathcal{D}_{1}\) parallèles.
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(2= \frac{1}{3} \times 1 + p\) équivaut à \(\frac{5}{3} = p\).
Equation de cette droite : \(y=\frac{1}{3}x+\frac{5}{3}\).
Equation de la droite \(\mathcal{D}_{2}\) passant par \(A(1,2)\) et parallèle à l'axe des abscisses \((OI)\) :
Coefficient directeur : il est égal à \(0\), celui de l'axe des abscisses car \(\mathcal{D}_{1}\) et \((OJ)\) sont parallèles.
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(2= 0 \times 1 + p\) équivaut à \(2 = p\).
Equation de cette droite : \(y=2\).
Equation de la droite \(\mathcal{D}_{3}\) passant par \(A(1,2)\) et parallèle à l'axe des ordonnées \((OJ)\) :
La droite \(\mathcal{D}_{3}\) n'a donc pas de coefficient directeur et une équation du type \(x=k\).
\(A\) appartient à la droite \(\mathcal{D}_{3}\) : \(x_{A}=k\) équivaut à \(1 =k\).
Equation de cette droite : \(x=1\).
Ex7 Dans un repère (O, I, J),soit les points \(A(-3,4)\), \(B(-1,-2)\) et \(C(-\frac{1}{2}, \frac{3}{2})\)
Equation de la médiane \(\Delta\) issue de \(A\) dans le triangle \(ABC\) :
On calcule d'abord les coordonnées du milieu \(E\) de \([BC]\) : \(E\left(\frac{-1-\frac{1}{2}}{2}, \frac{-2+\frac{3}{2}}{2} \right)\) donc \(E\left(-\frac{3}{4}, -\frac{1}{4} \right)\)
La médiane \(\Delta\) est la droite \((AE)\) :
Coefficient directeur : \(m=\frac{-\frac{1}{4}-4}{-\frac{3}{4}-(-3)}=-\frac{17}{9}\).
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(4= -\frac{17}{9} \times (-3) + p\) équivaut à \(-\frac{5}{3}= p\).
Equation de cette droite \(\Delta\) : \(y=-\frac{17}{9}x-\frac{5}{3}\).
Soit le point \(D(3,-7)\) : \(-\frac{17}{9}x_{D}-\frac{5}{3}=-\frac{17}{3}-\frac{5}{3}=-\frac{22}{3} \neq y_{D}\). Donc le point \(D\) n'appartient pas à la médiane \(\Delta\).
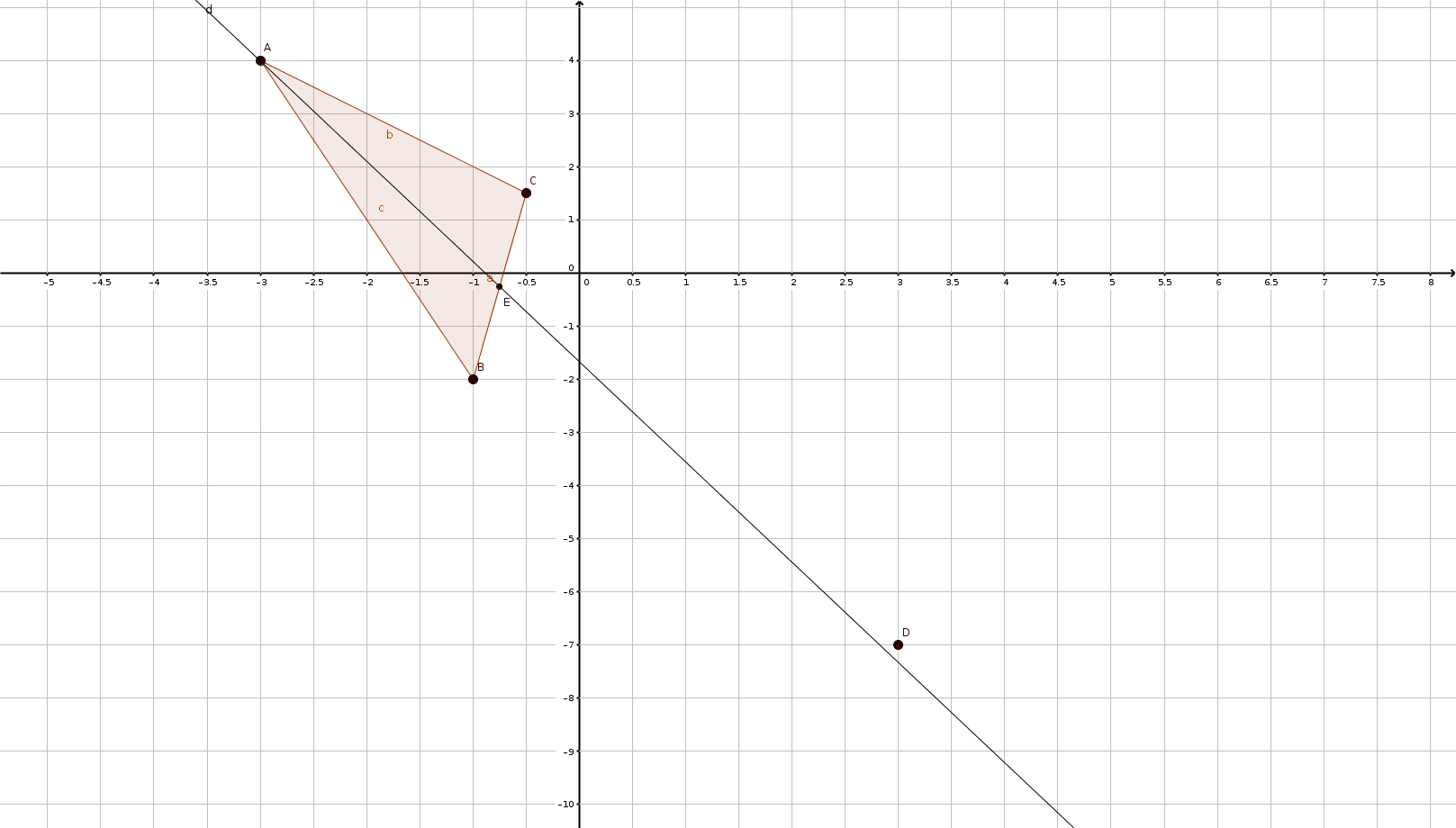
Figure de l'ex7
Ex8 Dans un repère (O, I, J),soit les points \(A(6,-1)\) \(B(-12,-13)\) \(C(252,70)\) et \(D(-45,-35)\).
Coefficient directeur de la droite \((AB)\) : \(m_{1}=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{-13-(-1)}{-12-6}=\frac{-12}{-18}=\frac{2}{3}\)
Coefficient directeur de la droite \((AC)\) : \(m_{2}=\frac{y_{C}-y_{A}}{x_{C}-x_{A}}=\frac{70-(-1)}{252-6}=\frac{71}{246}\)
Coefficient directeur de la droite \((AD)\) : \(m_{3}=\frac{y_{D}-y_{A}}{x_{D}-x_{A}}=\frac{-35-(-1)}{-45-6}=\frac{34}{51}=\frac{2}{3}\)
Les coefficients directeurs de \((AB)\) et \((AD)\) sont égaux donc ces droites sont parallèles. Ces deux droites ont un point commun \(A\), elles sont donc confondues et les points \(A\), \(B\) et \(D\) sont alignés.
Les coefficients directeurs de \((AB)\) et \((AC)\) sont différents (comparer leurs formes irréductibles) donc \((AB)\) et \((AC)\) sont sécantes en \(A\) et les points \(A\), \(B\) et \(C\) ne sont pas alignés.
Déterminons une équation de la droite \((AB)\) avec \(A(6,-1)\) et \(B(-12,-13)\) :
Coefficient directeur déjà calculé : \(m=\frac{2}{3}\)
Ordonnée à l'origine : \(y_{A}=mx_{A}+p\) équivaut à \(-1=\frac{2}{3} \times 6 + p\) équivaut à \(p=-5\)
Equation de \((A)\) : \(y=\frac{2}{3}x-5\)
On vérifie que \(D(-45,-35)\) appartient à la droite \((AB)\) car \(y_{D}=\frac{2}{3}x_{D}-5\)
On vérifie que \(C(252,70)\) n'appartient pas à la droite \((AB)\) car \(y_{C} \neq \frac{2}{3}x_{C}-5\)
Ex9 Dans un repère (O, I, J),soit les points \(E(56,19)\) \(F(38,7)\) \(G(-16,5)\) et \(H(314,225)\)
Coefficient directeur de la droite \((EF)\) : \(m_{1}=\frac{7-19}{38-56}=\frac{-12}{-18}=\frac{2}{3}\)
Coefficient directeur de la droite \((GH)\) : \(m_{2}=\frac{225-5}{314-(-16)}=\frac{220}{330}=\frac{2}{3}\)
Coefficient directeur de la droite \((EG)\) : \(m_{3}=\frac{5-19}{-16-56}=\frac{7}{36}\)
Coefficient directeur de la droite \((FH)\) : \(m_{4}=\frac{225-7}{314-38}=\frac{109}{138}\)
Les coefficients directeurs de \((EF)\) et \((GH)\) sont égaux donc ces droites sont parallèles.
Les coefficients directeurs de \((EG)\) et \((FH)\) sont différents donc ces droites sont sécantes.
Ex10 Dans le plan muni d'un repère,soit les points \(R(-5,-2)\) \(S(5,28)\) \(T(-1,8)\)
Coordonnées du milieu \(I\) de \([ST]\) : \(I\left( \frac{5+(-1)}{2}, \frac{28+8}{2} \right)\) donc \(I\left( 2, 18 \right)\)
Coordonnées du milieu \(J\) de \([RT]\) : \(J\left( \frac{-5+(-1)}{2}, \frac{(-2)+8}{2} \right)\) donc \(I\left( -3, 3\right)\)
La médiane issue de \(R\) dans le triangle \(RST\) est la droite \((RI)\) :
Coefficient directeur : \(m=\frac{18-(-2)}{2-(-5)}=\frac{20}{7}\)
Ordonnée à l'origine : \(y_{R}=mx_{R}+p\) équivaut à \(-2= \frac{20}{7} \times (-5) + p\) équivaut à \(\frac{86}{7} = p\).
Equation de cette droite : \(y=\frac{20}{7}x+\frac{86}{7}\).
La médiane issue de \(S\) dans le triangle \(RST\) est la droite \((SJ)\) :
Coefficient directeur : \(m=\frac{28-3}{5-(-3)}=\frac{25}{8}\)
Ordonnée à l'origine : \(y_{S}=mx_{S}+p\) équivaut à \(28= \frac{25}{8} \times 5 + p\) équivaut à \(\frac{99}{8} = p\).
Equation de cette droite : \(y=\frac{25}{8}x+\frac{99}{8}\).
Le centre de gravité \(G\) du triangle \(RST\) est le point d'intersection des médianes \((RI)\) et \((SJ)\), ses coordonnées \((x, y)\) sont donc solutions du système : \[\begin{cases} y=\frac{20}{7}x+\frac{86}{7} \\ y=\frac{25}{8}x+\frac{99}{8} \end{cases}\]
En résolvant ce système par substitution, on trouve que les coordonnées de \(G\) sont \(\left(-\frac{1}{3}, \frac{34}{3} \right)\).
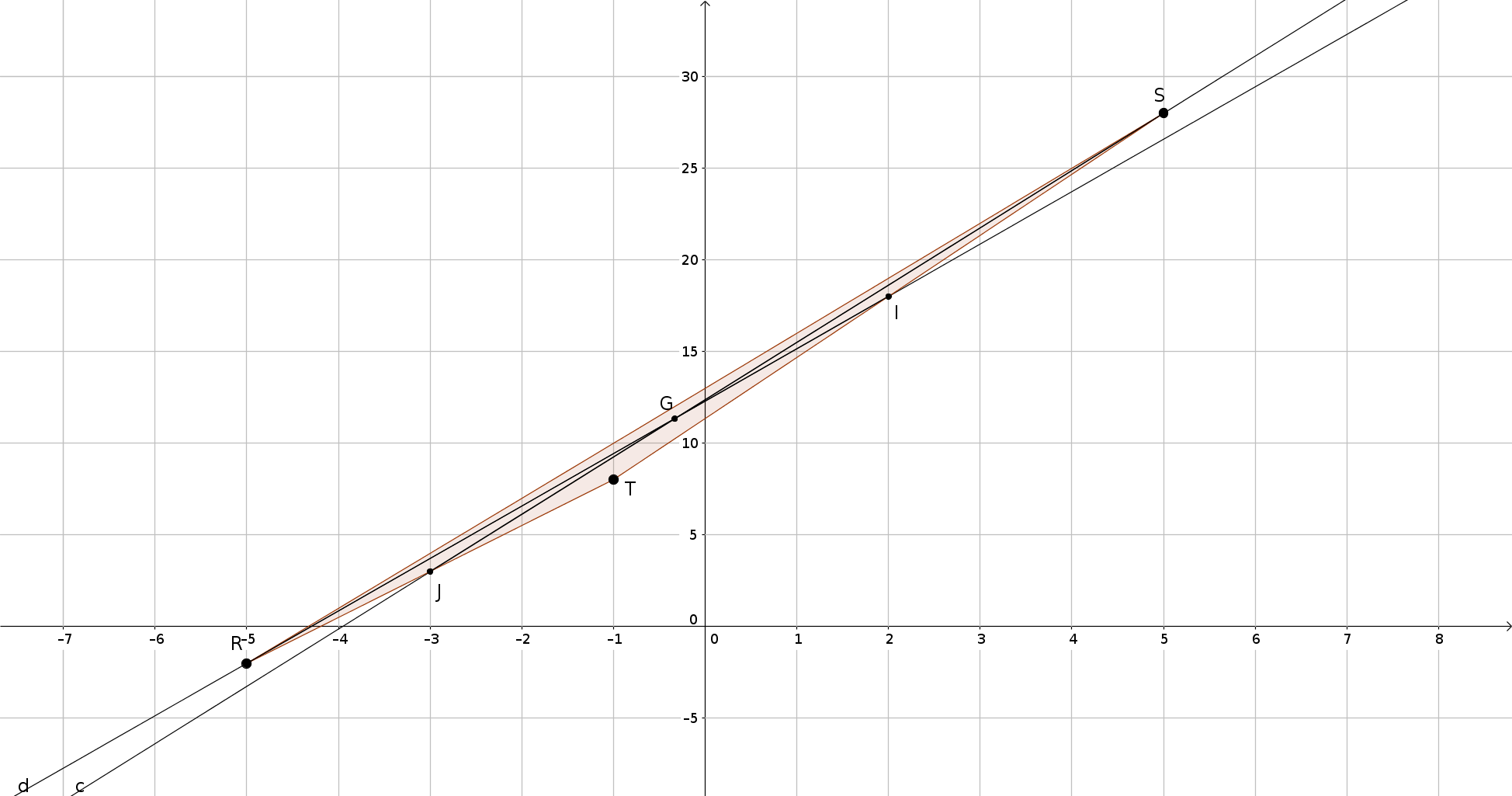
Figure de l'ex10